MF矩阵分解

• 1.解决问题
• 2.解决思路
• 3.潜在问题
• 4.矩阵分解的方式
• • 4.1 特征值分解【只适用于方阵】
  • 4.2 奇异值分解SVD，Singular Value Decomposition】
  • 4.3 Basic SVD
  • 4.4 RSVD
  • 4.5 SVD++
• 5.MF局限性
• 6.代码解析
• • 6.1 初代MF代码过程
  • 6.2 进阶SVD++
  • • 6.2.1 用户评分历史物品数量
    • 6.2.2初始化物品与物品相互影响因子矩阵中分解矩阵之一
    • 6.2.3计算物品相似度矩阵
    • • 6.2.3.1构建倒排表
      • 6.2.3.2统计每个物品有行为的用户数
      • 6.2.3.3构造同现矩阵
      • 6.2.3.4计算物品之间的相似度
  • 6.3 针对6.2改进
  • • 6.3.1初始化物品与物品相互影响因子矩阵中分解矩阵之一为Y矩阵
    • 6.3.2初始化偏置以及计算评分数量
    • 6.3.3随机模型
    • 6.3.4随机梯度下降
    • 6.3.5梯度更新
• 7.实验结果与分析(运行结果截图、分析与方法比较)
• 8.完整代码
• 9.参考

矩阵分解算法MF

1.解决问题

• 协同过滤处理稀疏矩阵的能力比较弱
• 协同过滤中，相似度矩阵维护难度大【m * m，n*n】

2.解决思路

使用隐向量【潜在信息】给原矩阵分解

3.潜在问题

• 矩阵是稀疏的
• 隐含特征不可知，是通过训练模型，让模型自行学习

4.矩阵分解的方式

4.1 特征值分解【只适用于方阵】

4.2 奇异值分解SVD，Singular Value Decomposition】

缺点:

• 传统的SVD分解要求原始矩阵是稠密的【如果想用奇异值分解，就必须对缺失的元素进行填充，而补全空间复杂度会非常高，且补的不一定准确】
• SVD分解计算复杂度非常高，而用户-物品矩阵很大

4.3 Basic SVD

4.4 RSVD

4.5 SVD++

5.MF局限性

• 无法利用用户特征、物品特征、上下文特征
• 缺乏用户历史行为时无法推荐

6.代码解析

6.1 初代MF代码过程

6.2 进阶SVD++

为更好叙述过程此处采取小矩阵数据集进行介绍，SVD++重点是在初代MF基础上融入用户评过分的历史物品，具体公式如下图

进一步优化公式如下图

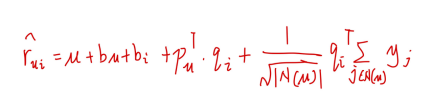
6.2.1 用户评分历史物品数量

6.2.2初始化物品与物品相互影响因子矩阵中分解矩阵之一

6.2.3计算物品相似度矩阵

电影1电影2电影3电影4

用户1 5 3 0 1
用户2 4 0 0 1
用户3 1 1 0 5
用户4 1 0 0 4
用户5 0 1 5 4

6.2.3.1构建倒排表

通过遍历每一个用户评分记录，获取评分不为0的电影下标+1,从而得到用户物品倒排表inverted👇
用户1 电影124
用户2 电影14
用户3 电影124
用户4 电影14
用户5 电影234
实现结果👇

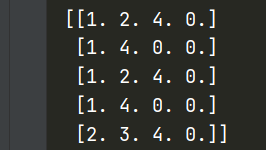
代码👇

6.2.3.2统计每个物品有行为的用户数

每个电影被参与评分的用户人数
结果👇

代码👇

6.2.3.3构造同现矩阵

通过用户物品倒排表计算同时喜欢两个物品的用户数,目标矩阵如下表
电影1 电影2 电影3 电影4
电影1 0 2 0 4
电影2 2 0 1 3
电影3 0 1 0 1
电影4 4 3 1 0
实现结果👇【获取组合数】
[(1.0, 2.0), (1.0, 4.0), (2.0, 1.0), (2.0, 4.0), (4.0, 1.0), (4.0, 2.0), (1.0, 4.0), (4.0, 1.0), (1.0, 2.0), (1.0, 4.0), (2.0, 1.0), (2.0, 4.0), (4.0, 1.0), (4.0, 2.0), (1.0, 4.0), (4.0, 1.0), (2.0, 3.0), (2.0, 4.0), (3.0, 2.0), (3.0, 4.0), (4.0, 2.0), (4.0, 3.0)]

代码👇
寻找所有用户的已评分电影的组合数代码

统计组合数并映射成矩阵(即同现矩阵)
结果👇

代码👇

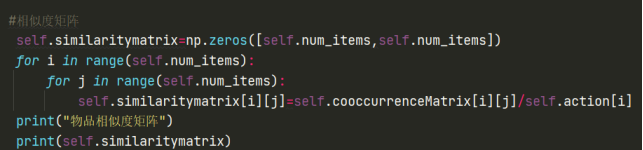
6.2.3.4计算物品之间的相似度

根据公式

分子: 同时喜欢电影i与电影j的用户数
分母: 喜欢电影i的用户数
利用上述所求cooccurrenceMatrix矩阵(含同时喜欢电影i与电影j的用户数)以及action(含喜欢电影i的用户数)

结果👇

代码👇

历史物品影响因子矩阵(5*4)👇

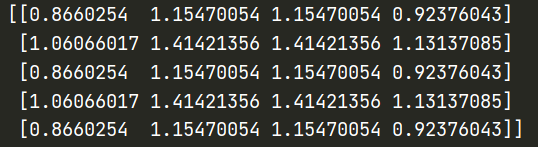
代码👇

影响因子矩阵加入至梯度更新👇

6.3 针对6.2改进

在代码更换数据集为movielens后，采用6.2过程发现，跑一晚也未抛出结果，对此检查发现，忽视掉了数据集矩阵为0时，是矩阵为空的情况，而不等同于评分为0，所以不可通过6.2过程中的计算方式得到物品与物品的相似度矩阵。更改后，在6.1版本的基础下增加如下过程

6.3.1初始化物品与物品相互影响因子矩阵中分解矩阵之一为Y矩阵

6.3.2初始化偏置以及计算评分数量

6.3.3随机模型

6.3.4随机梯度下降

6.3.5梯度更新

7.实验结果与分析(运行结果截图、分析与方法比较)

SVD++结果👇
迭代30次

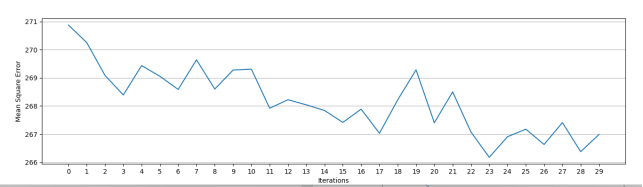
迭代100次

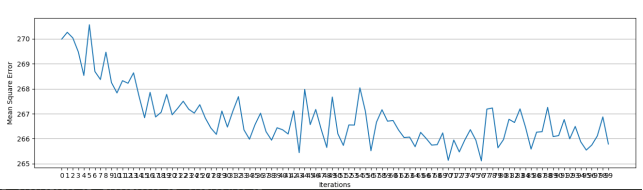
RSVD结果👇
迭代30次

针对RSVD与SVD++比较，SVD＋＋融入了用户对历史评分的影响，利于模型预测的准确性，收敛更光滑，对此svd++对于本数据集而言有增强推荐效果

8.完整代码

import numpy as npimport matplotlibimport matplotlib.pyplot as pltimport numpy as npimport mathimport pandas as pdfrom openpyxl import load_workbookclass Reader:    """    可读取的文件格式: .csv .tsv .xlsx .xlx .txt    """    @staticmethod    def read_csv(path): """ 读取.csv或.tsv文件 :param path:文件路径 :return:二维数组 """ array = pd.read_csv(path, header=None) np_array = np.array(array) return np_arrayclass MF(): def __init__(self, R, K, alpha, beta, iterations): """  Arguments - R (ndarray)   : user-item rating matrix - K (int): number of latent dimensions - alpha (float) : learning rate - beta (float)  : regularization parameter """  self.R = R self.num_users, self.num_items = R.shape self.K = K self.alpha = alpha self.beta = beta self.iterations = iterations    def train(self): # Initialize user and item latent feature matrice # 初始化用户和物品的潜在特征矩阵 # scale：float此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高） # size：int or tuple of ints # 输出的shape，默认为None，只输出一个值 #  np.random.randn(size)为标准正态分布（μ = 0, σ = 1），对应于np.random.normal(loc=0, scale=1, size) self.P = np.random.normal(scale=1./self.K, size=(self.num_users, self.K)) self.Q = np.random.normal(scale=1./self.K, size=(self.num_items, self.K)) # 初始化物品与物品相互影响因子矩阵中分解矩阵之一为Y矩阵 self.Y = np.random.normal(scale=1. / self.K, size=(self.num_items, self.K)) # 初始化偏置 self.b_u = np.zeros(self.num_users) self.b_i = np.zeros(self.num_items) self.b = np.mean(self.R[np.where(self.R != 0)])# 全局平均数 self.K=np.zeros([self.num_items,self.num_items]) # 初始化偏置 self.b_u2 = np.zeros(self.num_items) self.b_i2 = np.zeros(self.num_items) self.b2 = np.mean(self.K[np.where(self.K != 0)])  # 全局平均数 # 用户u评分物品的数量 self.N_u=np.zeros(self.num_users) for i in range(self.num_users):     for j in range(self.num_items):  if R[i][j]>0:      self.N_u[i]+=1 # print(self.N_u)# [3. 2. 3. 2. 3.] for j in range(len(self.N_u)):     self.N_u[j] =1/ math.sqrt(self.N_u[j]) print(self.N_u) self.samples = [     (i, j, self.R[i, j])     for i in range(self.num_users)     for j in range(self.num_items)     if self.R[i, j] > 0 ] self.samples2 = [     (i, j, self.K[i, j])     for i in range(self.num_items)     for j in range(self.num_items)     if self.K[i, j] > 0 ] # #执行随机梯度下降迭代次数 training_process = [] for i in range(self.iterations):     np.random.shuffle(self.samples)#随机打乱     np.random.shuffle(self.samples2)#随机打乱     # self.similarityMatrix()     # self.correlationFactor()     self.sgd2()     self.sgd()     mse = self.mse()     training_process.append((i, mse))     if (i+1) % 10 == 0:  print("Iteration: %d ; error = %.4f" % (i+1, mse))  return training_process # 物品与物品相似度计算    # def similarityMatrix(self):    #     # 用户物品倒排表    #     self.inverted = np.zeros([self.num_users, self.num_items])    #     for i in range(self.num_users):    #  k = 0    #  for j in range(self.num_items):    #      if R[i][j] > 0:    #   self.inverted[i][k] = j+1    #   k += 1    #     print(self.inverted)#[1. 2. 4. 0.][1. 4. 0. 0.] [1. 2. 4. 0.] [1. 4. 0. 0.][2. 3. 4. 0.]    #    #     # 统计每个物品有行为的用户数    #     self.action = np.zeros(self.num_items)    #     for i in range(self.num_items):    #  k = 0    #  for j in range(self.num_users):    #      if R[j][i] > 0:    #   self.action[i]=k+1    #   k += 1    #     print(self.action)#[4. 3. 1. 5.]    #    #     #同现矩阵    #     self.cooccurrenceMatrix=np.zeros([self.num_items, self.num_items])    #     self.connect=[]    #     for i in range(self.num_users):#寻找所有用户的已评分电影的组合数    #  for k in range(self.num_items):    #      if self.inverted[i][k]!=0:    #   for j in range(self.num_items):    #if self.inverted[i][k]!=self.inverted[i][j]:    #    if self.inverted[i][j] > 0:    # self.connect.append((self.inverted[i][k],self.inverted[i][j]))    #     self.countitem={}    #     for i in self.connect:    #    self.countitem[i] = self.connect.count(i)    #     # print(self.countitem)#{(1.0, 2.0): 2, (1.0, 4.0): 4, (2.0, 1.0): 2, (2.0, 4.0): 3, (4.0, 1.0): 4, (4.0, 2.0): 3, (2.0, 3.0): 1, (3.0, 2.0): 1, (3.0, 4.0): 1, (4.0, 3.0): 1}    #     # 统计组合数并映射成矩阵(即同现矩阵)    #     for i in range(len(self.countitem)):    #  a=list(self.countitem.keys())[i][0]-1    #  b=list(self.countitem.keys())[i][1]-1    #  self.cooccurrenceMatrix[int(a),int(b)]=list(self.countitem.values())[i]    #     # print(self.cooccurrenceMatrix)#[[0. 2. 0. 4.][2. 0. 1. 3.] [0. 1. 0. 1.] [4. 3. 1. 0.]]    #    #    #相似度矩阵    #     self.similaritymatrix=np.zeros([self.num_items,self.num_items])    #     for i in range(self.num_items):    #  for j in range(self.num_items):    #      self.similaritymatrix[i][j]=self.cooccurrenceMatrix[i][j]/self.action[i]    #     print("物品相似度矩阵")    #     print(self.similaritymatrix)    # #历史物品影响因子矩阵(5*4)    # def correlationFactor(self):    #     self.correlation_factor=np.zeros([self.num_users,self.num_items])    #     for i in range(self.num_users):    #  for j in range(self.num_items):    #      for k in range(self.num_items):    #   self.correlation_factor[i][j]+=self.similaritymatrix[j][k]    #      self.correlation_factor[i][j]=self.correlation_factor[i][j]*self.N_u[i]    #     print("历史物品影响因子矩阵(5*4)")    #     print(self.correlation_factor)    def mse(self): xs, ys = self.R.nonzero() predicted = self.full_matrix() error = 0 for x, y in zip(xs, ys):     error += pow(self.R[x, y] - predicted[x, y], 2) return np.sqrt(error)    def sgd(self): """ sgd随机梯度下降 """ for i, j, r in self.samples:     prediction = self.get_rating(i, j)     e = (r - prediction)     self.b_u[i] += self.alpha * (e - self.beta * self.b_u[i])     self.b_i[j] += self.alpha * (e - self.beta * self.b_i[j])     # 创建行P的副本，因为我们需要更新它，但使用旧的值更新Q     P_i = self.P[i, :][:]     self.P[i, :] += self.alpha * (e * self.Q[j, :] - self.beta * self.P[i,:])     self.Q[j, :] += self.alpha * (e * P_i - self.beta * self.Q[j,:])    def sgd2(self): """ sgd随机梯度下降 """ for i, j, r in self.samples2:     prediction2 = self.get_rating2(i, j)     e2 = (r - prediction2)     self.b_u2[i] += self.alpha * (e2 - self.beta * self.b_u2[i])     self.b_i2[j] += self.alpha * (e2 - self.beta * self.b_i2[j])     # 创建行P的副本，因为我们需要更新它，但使用旧的值更新Q     Q_i = self.Q[i, :][:].T     self.Q[i, :].T += self.alpha * (e2 * self.Y[j, :] - self.beta * self.Q[i,:].T)     self.Y[j, :] += self.alpha * (e2 * Q_i - self.beta * self.Y[j,:])    def get_rating(self, i, j): prediction = self.b + self.b_u[i] + self.b_i[j] + self.P[i, :].dot(self.Q[j, :].T)+self.N_u[i]*self.Q[j, :].dot(self.Y[i,:].T)# +self.correlation_factor[i,j] return prediction    def get_rating2(self, i, j): prediction2 = self.b2 + self.b_u2[i] + self.b_i2[j] + (self.Q[i, :].T).dot(self.Y[j, :]) # +self.correlation_factor[i,j] return prediction2    def full_matrix(self): # np.newaxis的作用是增加一个维度。对于[:, np.newaxis]和[np.newaxis，：]是在np.newaxis这里增加1维 return self.b + self.b_u[:,np.newaxis] + self.b_i[np.newaxis:,] + self.P.dot(self.Q.T).dot(self.Y.dot(self.Q.T))R = np.array([    [5, 3, 0, 1],    [4, 0, 0, 1],    [1, 1, 0, 5],    [1, 0, 0, 4],    [0, 1, 5, 4],])# reader = Reader()   # 实例化# path = './traindataset.csv'    # 路径# R = reader.read_csv(path)mf = MF(R, K=2, alpha=0.1, beta=0.29, iterations=100)training_process = mf.train()print()print("P x Q:")print(mf.full_matrix())print()print("Global bias:")print(mf.b)print()print("User bias:")print(mf.b_u)print()print("Item bias:")print(mf.b_i)x = [x for x, y in training_process]y = [y for x, y in training_process]plt.figure(figsize=((16,4)))plt.plot(x, y)plt.xticks(x, x)plt.xlabel("Iterations")plt.ylabel("Mean Square Error")plt.grid(axis="y")plt.show()

9.参考

学习，讲得超级无敌好的up主