树

基本概念

1、树的概念

树是一种非线性的数据结构，是递归定义的。
注： 子树不能有交集，会变为图。

2、树的相关概念

节点的度： 一个节点含有的子树的个数称为该节点的度； 如上图：A的为6
叶节点或终端节点： 度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点
非终端节点或分支节点： 度不为0的节点； 如上图：D、E、F、G…等节点为分支节点
双亲节点或父节点： 若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点
孩子节点或子节点： 一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点
兄弟节点： 具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点
树的度： 一棵树中，最大的节点的度称为树的度； 如上图：树的度为6
节点的层次： 从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度： 树中节点的最大层次； 如上图：树的高度为4
堂兄弟节点： 双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
节点的祖先： 从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
子孙： 以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
森林： 由m（m>0）棵互不相交的树的集合称为森林；

树的表示

常用孩子兄弟表示法

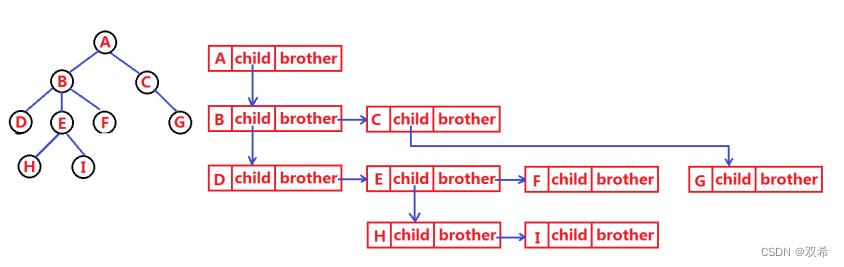
二叉树

是节点有限的集合。
要么为空，要么有左右孩子（子树（可为空））。

特殊的树

1、满二叉树：每层节点到达最大值。
设有h层，则此类树有2^h-1个节点。
2、完全二叉树：如图所示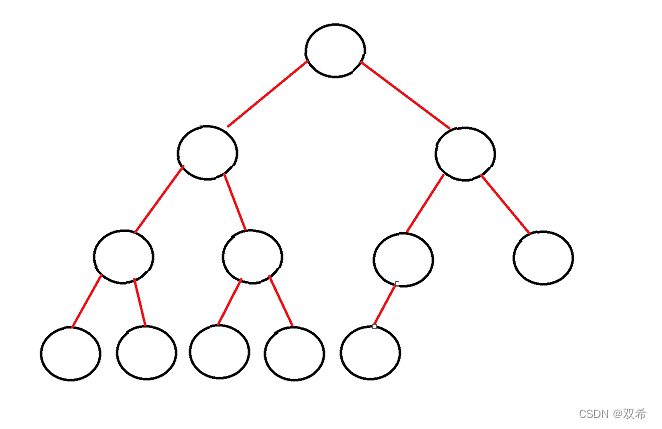

二叉树性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是 2^h-1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为 n2,则有 n0 ＝ n2＋1.

证明：

设总结点数n.
二叉树边数 = n-1；
二叉树结点贡献边数 = n1+2n2；
n0+n1+n2-1 = n1+2n2;
n0 = n2 + 1;

4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h= log 2 (n+1). (ps： log 2 (n+1) 是log以2为底，n+1为对数)

树的存储方式

顺序存储（主要用于堆）

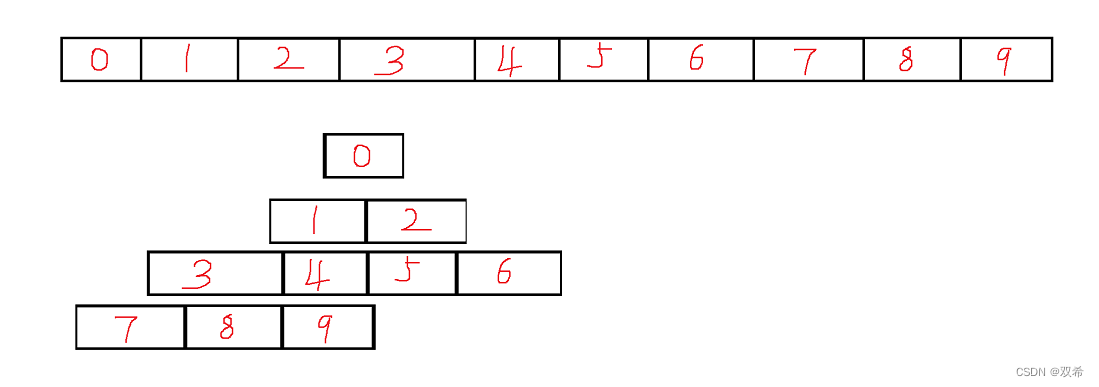
由上图可看出父子关系
parent = (child - 1)/2;
le_child = parent *2 + 1;
ri_child = parent *2 + 2;

链式存储

神漫画