从API角度彻底理解冒泡排序、选择排序、插入排序
从API角度彻底理解冒泡排序、选择排序、插入排序
-
- Comparable接口介绍
- 冒泡排序
-
- 冒泡排序API设计:
- 冒泡排序的时间复杂度分析
- 选择排序
-
- 选择排序API设计:
- 选择排序的时间复杂度分析
- 插入排序
-
- 插入排序API设计
- 插入排序的时间复杂度分析
只要你自己不倒下,就没人能让你倒下。只要你自己不认输,就没人能打败你。人活着就应该像齐天大圣,疯过,爱过,恨过,闯过,拼过,努力过,但从来没怕过。 ------共勉。
后续持续更新中…
Comparable接口介绍
说到排序,所以肯定会在元素之间进行比较,而Java提供了一个接口Comparable就是用来定义排序规则的,在这里我们以案例的形式对Comparable接口做一个简单的回顾。
需求:
1.定义一个学生类Student,具有年龄age和姓名username两个属性,并通过Comparable接口提供比较规则;
2.定义测试类Test,在测试类Test中定义测试方法Comparable getMax(Comparable c1,Comparable c2)完成测试
//学生类 package com.it.demo1;public class Student implements Comparable<Student>{ private String username; private int age; public void setUsername(String username) { this.username = username; } public void setAge(int age) { this.age = age; } public String getUsername() { return username; } public int getAge() { return age; } @Override public String toString() { return "Student{" + "username='" + username + '\'' + ", age=" + age + '}'; }//定义比较规则 @Override public int compareTo(Student o) { return this.getAge()-o.getAge(); }}//测试类public class StudentDemo { public static void main(String[] args) { Student v1 = new Student(); v1.setUsername("zhangsan"); v1.setAge(12); Student v2 = new Student(); v2.setUsername("zhangsanw"); v2.setAge(22); Comparable max = getMax(v1, v2); System.out.println(max); }//测试方法,获取两个元素中的较大值public static Comparable getMax(Comparable c1,Comparable c2){ int cmp = c1.compareTo(c2); if (cmp>=0){ return c1; }else{return c2; } } }冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
需求:
排序前:{4,5,6,3,2,1}
排序后:{1,2,3,4,5,6}
排序原理:
- 比较相邻的元素。如果前一个元素比后一个元素大,就交换这两个元素的位置。
- 对每一对相邻元素做同样的工作,从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大
值。

冒泡排序API设计:
| 类名 | Bubble |
|---|---|
| 构造方法 | Bubble():创建Bubble对象 |
| 成员方法 | 1.public static void sort(Comparable[] a):对数组内的元素进行排序 2.private static boolean greater(Comparable v,Comparable w):判断v是否大于w 3.private static void exch(Comparable[] a,int i,int j):交换a数组中,索引i和索引j处的值 |
冒泡排序的代码实现:
public class Bubble { /* 对数组a中的元素进行排序 */ public static void sort(Comparable[] a) { for (int i= a.length-1;i>0;i--){ for (int j = 0; j <=i-1 ; j++) { if (greater(a[j],a[j+1])){ exch(a,j,j+1); } } } } /* 比较v元素是否大于w元素 */ private static boolean greater(Comparable v,Comparable w){ return v.compareTo(w)>0; } /*数组元素i和j交换位置 */ private static void exch(Comparable[]a,int i,int j){ Comparable t = a[i]; a[i]=a[j]; a[j]=t; }}//测试代码public class BubbleDeom { public static void main(String[] args) { Integer[] a={3,4,1,6,8,2}; Bubble.sort(a); System.out.println(Arrays.toString(a)); System.out.println(Arrays.toString(a)); }}冒泡排序的时间复杂度分析
冒泡排序使用了双层for循环,其中内层循环的循环体是真正完成排序的代码,所以,我们分析冒泡排序的时间复杂度,主要分析一下内层循环体的执行次数即可。
在最坏情况下,也就是假如要排序的元素为{6,5,4,3,2,1}逆序,那么:
元素比较的次数为:
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
元素交换的次数为:
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
总执行次数为:
(N2/2-N/2)+(N2/2-N/2)=N^2-N;
按照大O推导法则,保留函数中的最高阶项那么最终冒泡排序的时间复杂度为O(N^2)
选择排序
选择排序是一种更加简单直观的排序方法。
需求:
排序前:{4,6,8,7,9,2,10,1}
排序后:{1,2,4,5,7,8,9,10}
排序原理:
1.每一次遍历的过程中,都假定第一个索引处的元素是最小值,和其他索引处的值依次进行比较,如果当前索引处的值大于其他某个索引处的值,则假定其他某个索引出的值为最小值,最后可以找到最小值所在的索引
2.交换第一个索引处和最小值所在的索引处的值
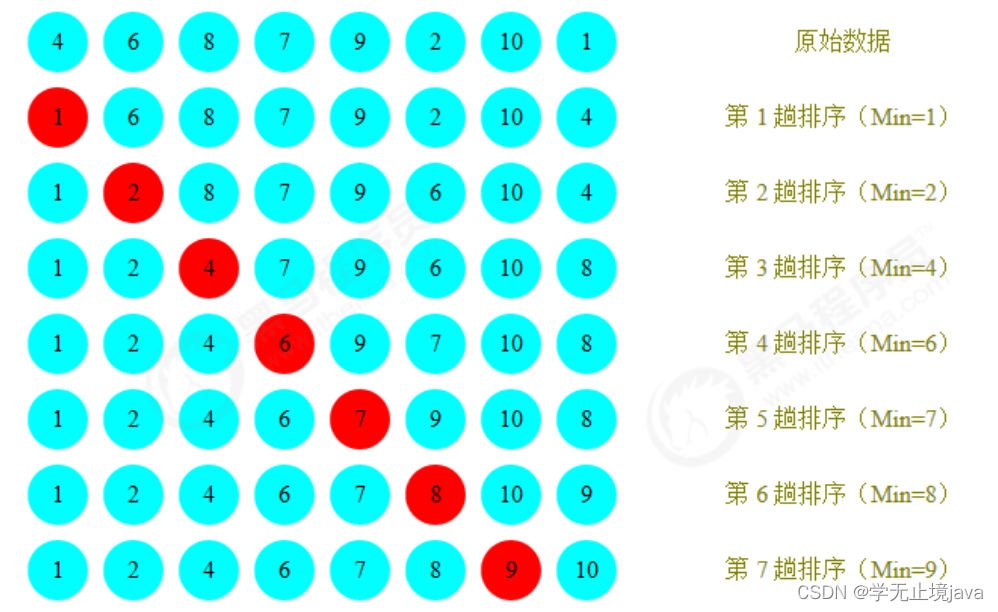
选择排序API设计:
| 类名 | Selection |
|---|---|
| 构造方法 | Selection():创建Selection对象 |
| 成员方法 | 1.public static void sort(Comparable[] a):对数组内的元素进行排序。 2.private static boolean greater(Comparable v,Comparable w):判断v是否大于w。 3.private static void exch(Comparable[] a,int i,int j):交换a数组中,索引i和索引j处的值 |
选择排序的代码实现:
/* 对数组a中的元素进行排序 */ public static void sort(Comparable[] a){ for (int i = 0; i <= a.length-2 ; i++) { //假定本次遍历,最小值所在的索引是i int minIndex=i; for (int j = i+1; j <a.length ; j++) { if (greater(a[minIndex],a[j])){ //跟换最小值所在的索引 minIndex=j; } } //交换i索引处和minIndex索引处的值 exch(a,i,minIndex); } } /* 比较v元素是否大于w元素 */ private static boolean greater(Comparable v,Comparable w){ return v.compareTo(w)>0; } /*数组元素i和j交换位置 */ private static void exch(Comparable[] a,int i,int j){ Comparable t = a[i]; a[i]=a[j]; a[j]=t; }}//测试代码 public class Test { public static void main(String[] args) { Integer[] a = {4,6,8,7,9,2,10,1}; Selection.sort(a); System.out.println(Arrays.toString(a)); } }选择排序的时间复杂度分析
选择排序使用了双层for循环,其中外层循环完成了数据交换,内层循环完成了数据比较,所以我们分别统计数据交换次数和数据比较次数:
数据比较次数:
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
数据交换次数:
N-1
时间复杂度:N2/2-N/2+(N-1)=N2/2+N/2-1;
根据大O推导法则,保留最高阶项,去除常数因子,时间复杂度为O(N^2);
插入排序
插入排序(Insertion sort)是一种简单直观且稳定的排序算法。
插入排序的工作方式非常像人们排序一手扑克牌一样。开始时,我们的左手为空并且桌子上的牌面朝下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较。
需求:
排序前:{4,3,2,10,12,1,5,6}
排序后:{1,2,3,4,5,6,10,12}
排序原理:
1.把所有的元素分为两组,已经排序的和未排序的;
2.找到未排序的组中的第一个元素,向已经排序的组中进行插入;
3.倒叙遍历已经排序的元素,依次和待插入的元素进行比较,直到找到一个元素小于等于待插入元素,那么就把待插入元素放到这个位置,其他的元素向后移动一位;

插入排序API设计
| 类名 | Insertion |
|---|---|
| 构造方法 | Insertion():创建Insertion对象 |
| 成员方法 | 1.public static void sort(Comparable[] a):对数组内的元素进行排序 。2.private static boolean greater(Comparable v,Comparable w):判断v是否大于w。3.private static void exch(Comparable[] a,int i,int j):交换a数组中,索引i和索引j处的值 |
插入排序代码实现:
public class Insertion { /* 对数组a中的元素进行排序 */ public static void sort(Comparable[] a){ for (int i = 1; i < a.length; i++) { //当前元素为a[i],依次和i前面的元素比较,找到一个小于等于a[i]的元素 for (int j = i; j > 0 ; j--) { if (greater(a[j-1],a[j])){ //交换元素 exch(a,j-1,j); }else { //找到了该元素,结束 break; } } } } /* 比较v元素是否大于w元素 */ private static boolean greater(Comparable v,Comparable w){ return v.compareTo(w)>0; } /*数组元素i和j交换位置 */ private static void exch(Comparable[] a,int i,int j){ Comparable t = a[i]; a[i]=a[j]; a[j]=t; }}插入排序的时间复杂度分析
插入排序使用了双层for循环,其中内层循环的循环体是真正完成排序的代码,所以,我们分析插入排序的时间复杂度,主要分析一下内层循环体的执行次数即可。
最坏情况,也就是待排序的数组元素为{12,10,6,5,4,3,2,1},那么:
比较的次数为:
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
交换的次数为:
(N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)(N-1)/2=N^2/2-N/2;
总执行次数为:
(N2/2-N/2)+(N2/2-N/2)=N^2-N;
按照大O推导法则,保留函数中的最高阶项那么最终插入排序的时间复杂度为O(N^2).


