Python每日一练-----只出现一次的计算
⛅(day21)
🖍题目:
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
🌠示例 1:
输入: [2,2,1]
输出: 1
🌠示例 2:
输入: [4,1,2,1,2]
输出: 4
题目分析:
如果没有算法应该具有线性时间复杂度,且不使用额外空间的要求相信大家都能做出来。对于这要求,线性时间复杂度是值O(n),这一位这你只能遍历一次数组。不使用额外的空间就要求不能使用新的数组,字典等储存相关信息。简单来说就是要求我们在只遍历一次数组的情况下找出单独出现的数字。
解题思路:
对于不使用额外空间,我们应该想到位运算。
简要介绍一下位运算符“ ^ ".
“ ^ "的运算规则为,当两个运算数不同时为1,相同时为0
例1
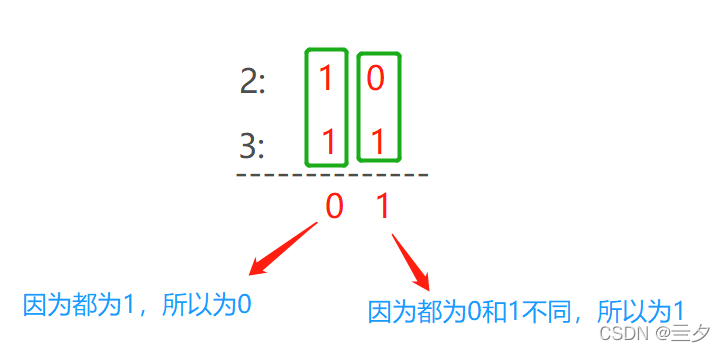
a = 2(对应的二进制表示为:10)
b = 3(对应的二进制表示为:11)
a^b = 2
运算过程如下
例2
a = 2(对应的二进制表示为:10)
b = 2(对应的二进制表示为:10)
a^b = 0
运算过程如下

例3
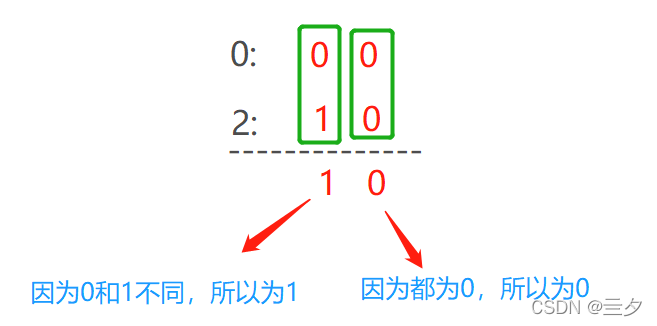
a = 0(对应的二进制表示为:00)
b = 2(对应的二进制表示为:10)
a^b = 2
运算过程如下
例4
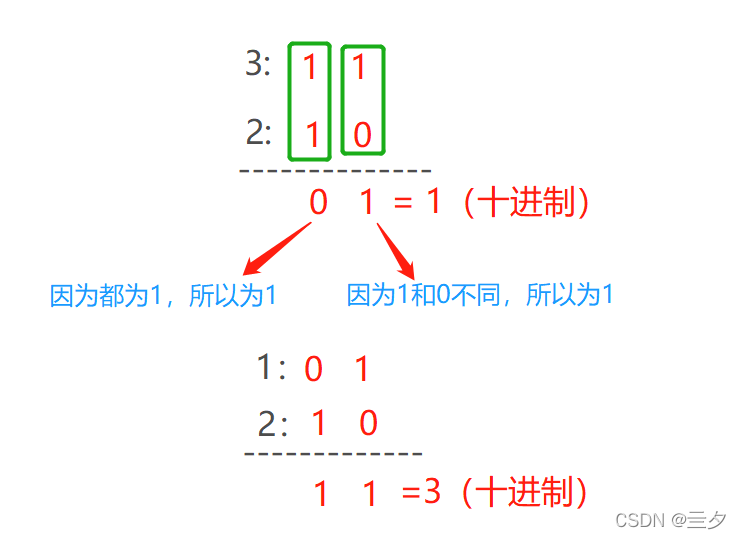
a = 3(对应的二进制表示为:11)
b = 1(对应的二进制表示为:0)
a^b^b = a = 3
运算过程如下
由上面的三个例题,可以知道,
- 当遍历数组时出现两个相同的数时,运算结果为0.
- 当0^任何数 = 任何数
- a^b^b=a
有a(只出现一次的数)b,c,.....(出现两次的数)
a^b^c^....=a
b^a^c^....=a
所以只需进行 a^b运算即可得所求的数
🌈代码实现
def singleNumber(nums): a = 0 for num in nums: a = a ^ num return a这样就满足了题目算法应该具有线性时间复杂度,且不使用额外空间的要求。
今天就到这,明天见。🚀
❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄end❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄