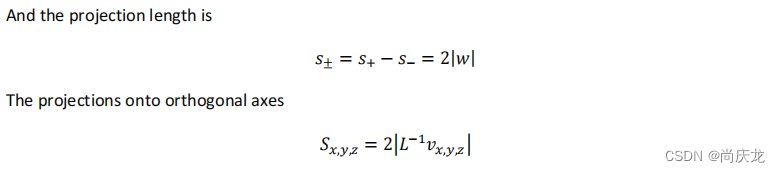利用毫米波雷达点云进行多目标聚类跟踪的算法设计
利用毫米波雷达点云进行多目标聚类跟踪的算法设计
文章目录
- 利用毫米波雷达点云进行多目标聚类跟踪的算法设计
-
- 前言
- 1 简介
-
- 1.1 跟踪模块
- 1.2 雷达几何图
- 1.3 跟踪坐标系的选择
- 1.4 恒速度模型(Constant Velocity Model)
- 1.5 恒加速度模型(Constant Acceleration Model)
- 2 卡尔曼滤波器操作
-
- 2.1 预测(Prediction)步骤
- 2.2 更新步骤
- 2.3 过程噪声矩阵 Q Q Q的设计
-
- 2.3.1 连续白噪声模型
- 2.3.2 分段白噪声模型(Piecewise White Noise Model)
- 3 群组跟踪(Group Tracking)
-
- 3.1 顶层算法设计
- 3.2 群组跟踪方框图
- 3.3 预测过程(Prediction Step)
- 3.4 关联过程(Association Step)
-
- 3.4.1 门限函数(Gating Function)
- 3.4.2 打分函数(Scoring Function)
- 3.5 分配过程(Allocation Step)
- 3.6 更新过程(Updating Step)
- 3.7 维持过程(Maintenance Step)
- 4 执行细节
-
- 4.1 群组跟踪器(Group Tracker)
- 4.2 配置参数
-
- 4.2.1 强制性的配置参数
- 4.2.2 高级参数
- 4.3 内存需求
-
- 4.3.1 Data Memory
- 4.3.2 Program Memory
- 4,4 BenchMarks
- 5 Performance
-
- 5.1 Tracking Reliability
-
- 5.1.1 Test Case描述
- 5.2 结论
- 5.2 Tracking Precision
-
- 5.2.1 测试case描述
- 5.3 Tracking Resolution
-
- 5.3.1 初始分离
- 5.3.2 动态分离
- 6 参考资料
- 7 Appendix
-
- 7.1 Evaluating Partial Derivatives
- 7.2 Orthogonal projection of an Ellipsoid E onto a given line
前言
本文主要参考TI官网TIDEP-0090短距毫米波雷达的设计实例,该实例主要用于交通目标对象的检测与跟踪。本文主要涉及其中的聚类和跟踪部分的算法设计。Ti官网相关网页请看:
【1】TIDEP-0090介绍
【2】本文的英文参考文档
1 简介
1.1 跟踪模块
在下图所示的雷达处理算法框架中,跟踪算法处于定位层(Localization)。跟踪器(Tracker)需要接收目标检测层(Detection)的输入,然后将定位信息提供给分类层(Classification)。
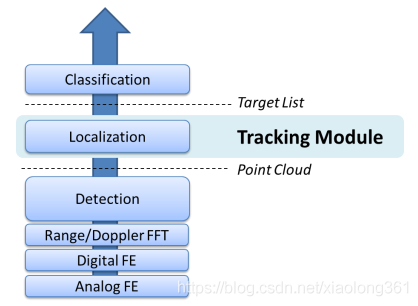
图1 雷达处理算法框架
借助高分辨率的毫米波雷达传感器,目标检测层(Detection)能够检测出实际物理目标的多反射点,并生成一组相应的测量结果, 在某些情况下每帧甚至可能有上千个测量结果,故我们将这些测量结果称之为“点云”。 每个测量结果代表一个反射点,包括径向距离、方位角以及径向速度等信息。另外, 测量结果还可能会包含信噪比等可靠性信息。
跟踪层需要根据输入的点云数据执行目标定位操作,并向分类层报告结果(一串目标列表(Target List))。因此,跟踪器的输出是一组可跟踪的目标,这些目标带有某些特定的属性(例如位置、速率、结构尺寸、点密度以及其他一些特征),可以被分类器进一步用于执行分类识别决策。
1.2 雷达几何图
下图展示了时刻 n n n时的单一反射点示意图。真实雷达目标一般由多个反射点组成。每个点都由径向距离(range)、角度(angle)和径向速度(radial velocity)组成:
- 径向距离(Range) r r r, R m i x < r <R m a xR_{mix}<r<R_{max} Rmix<r<Rmax
- 水平角(Azimuth Angle) φ \varphi φ,−ϕ m a x < φ < +ϕ m a x-\phi_{max}<\varphi<+\phi_{max} −ϕmax<φ<+ϕmax
- 径向速度(Radial Velocity) r˙ \dot{r} r˙
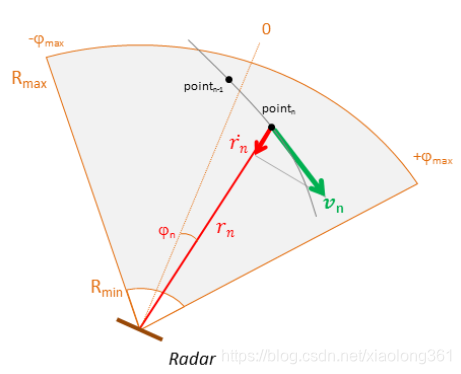
图2 2D雷达几何图
1.3 跟踪坐标系的选择
为了便于进行目标运动状态的推测估计,我们选择笛卡尔坐标系(直角坐标系)进行目标跟踪**——这使我们能够使用简单的牛顿线性预测模型**。为了避免误差多次耦合,我们选择将雷达测量值输入仍然保持在极坐标下。我们将使用扩展卡尔曼滤波器对跟踪的目标状态和测量向量之间的依赖关系进行线性化处理。
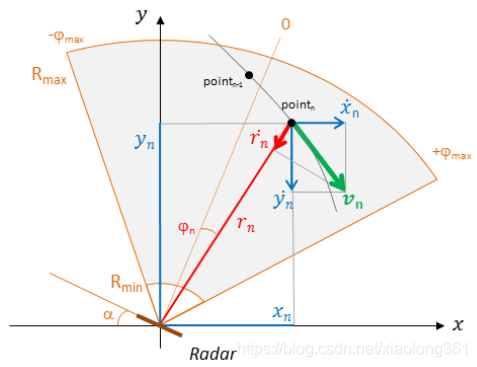
图3 在直角坐标系下进行目标跟踪
利用下式将极坐标转换为笛卡尔坐标:
x = r c o s ( π / 2 − ( α + φ ) ) = r s i n ( α + φ ) y = r s i n ( π / 2 − ( α + φ ) ) = r c o s ( α + φ ) x=rcos(\pi/2-(\alpha+\varphi))=rsin(\alpha+\varphi)\\ y=rsin(\pi/2-(\alpha+\varphi))=rcos(\alpha+\varphi) x=rcos(π/2−(α+φ))=rsin(α+φ)y=rsin(π/2−(α+φ))=rcos(α+φ)
我们的目的就是根据带有噪声的雷达测量值(距离range, 角度angle,径向速度radial velocity)来跟踪目标的位置。
1.4 恒速度模型(Constant Velocity Model)
我们使用卡尔曼滤波器来"重新定义"目标的位置估计,关于卡尔曼滤波器的基础教程可以参考本人的卡尔曼滤波器系列教程。卡尔曼滤波器在 n n n时刻的状态被定义为:
s ( n ) = F s ( n − 1 ) + w ( n ) s(n)=Fs(n-1)+w(n) s(n)=Fs(n−1)+w(n)
这里的状态向量 s ( n ) s(n) s(n)被定义在笛卡尔坐标系(直角坐标系)下:
s ( n ) = [ x ( n ) y ( n ) x˙ ( n ) y˙ ( n )]T s(n)= [x(n) \space y(n) \space\dot{x}(n) \space \dot{y}(n)]^T s(n)=[x(n) y(n) x˙(n) y˙(n)]T
F F F是转移矩阵:
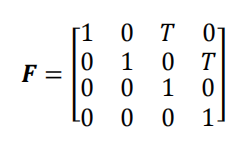
其中, w ( n ) w(n) w(n)是过程噪声向量,其协方差矩阵 Q ( n ) Q(n) Q(n)为一个 4 × 4 4\times 4 4×4矩阵。
输入测量向量 u ( n ) u(n) u(n)包括径向距离、角度和径向速度:
u ( n ) = [ r ( n ) φ ( n ) r˙ ( n )]T u(n)=[r(n) \space \varphi (n)\space\dot{r}(n)]^T u(n)=[r(n) φ(n) r˙(n)]T
卡尔曼滤波器的状态量 s ( n ) s(n) s(n)和测量向量 u ( n ) u(n) u(n)的相对关系用下式表示:
u ( n ) = H ( s ( n ) ) + v ( n ) u(n)=H(s(n))+v(n) u(n)=H(s(n))+v(n)
其中, H H H表示测量矩阵:
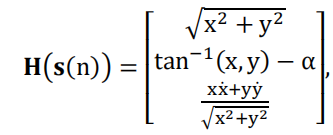
函数 t a n−1 ( x , y ) tan^{-1}(x,y) tan−1(x,y)定义为:
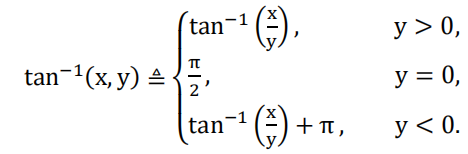
v ( n ) v(n) v(n)是测量噪声,其协方差矩阵 R ( n ) R(n) R(n)为一个 3 × 3 3\times 3 3×3矩阵。
在上述公式中,测量向量 u ( n ) u(n) u(n)和状态向量 s ( n ) s(n) s(n)之间具有非线性关系。为此,我们使用扩展卡尔曼滤波器(EKF)来简化 u ( n ) u(n) u(n)和 s ( n ) s(n) s(n)之间的关系。具体操作是只保留 H ( ⋅ ) H(\cdot) H(⋅)的一阶泰勒级数(数学原理可参考泰勒公式):
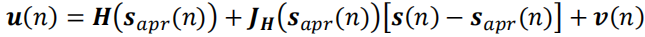
其中, sapr ( n ) s_{apr}(n) sapr(n)是状态向量在时刻 n n n基于时刻 n − 1 n-1 n−1的测量值得到的先验估计,
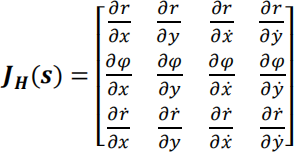
计算上式中的偏导数,得:
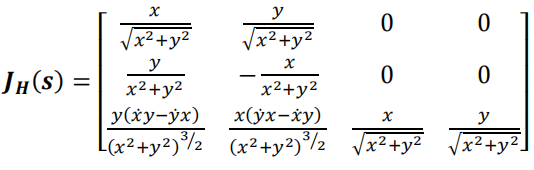
1.5 恒加速度模型(Constant Acceleration Model)
对于恒加速度模型,卡尔曼滤波器在 n n n时刻的状态被定义为:
s ( n ) = F s ( n − 1 ) + w ( n ) s(n)=Fs(n-1)+w(n) s(n)=Fs(n−1)+w(n)
其中,状态向量 s ( n ) s(n) s(n)定义在直角坐标系下:
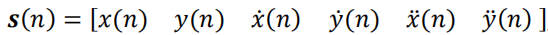
F F F表示状态转移矩阵:

其中, w ( n ) w(n) w(n)是过程噪声向量,其协方差矩阵 Q ( n ) Q(n) Q(n)为一个 6 × 6 6\times 6 6×6矩阵。
输入测量向量 u ( n ) u(n) u(n)和恒速度模型一样,包括径向距离、角度和径向速度:
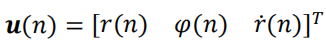
卡尔曼滤波器的状态向量和测量向量之间的关系如下:
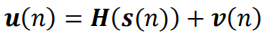
其中:
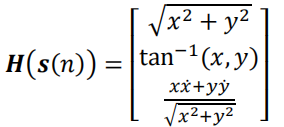
为了将状态向量和测量向量的关系线性化,我们执行以下的偏导数计算:
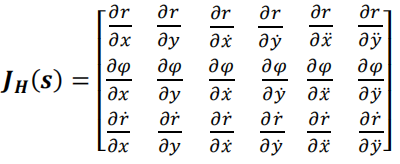
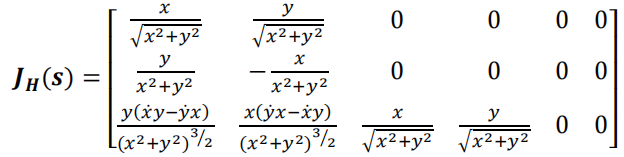
2 卡尔曼滤波器操作
首先对我们用到的符号进行说明:
- si ( n ) s_i(n) si(n)——正在跟踪的目标i i i在时刻n n n的状态向量。每个跟踪目标都有其状态向量,并且会被独立的预测和更新。
- s a p r ( n ) s_{apr}(n) sapr(n)——时刻n n n的跟踪状态的先验(预测)估计。
- P ( n ) P(n) P(n)——时刻n n n的状态向量预测误差协方差矩阵,定义为P ( n ) = C o v [ s ( n ) −s a p r ( n ) ] P(n)=Cov[s(n)-s_{apr}(n)] P(n)=Cov[s(n)−sapr(n)]。
- P a p r ( n ) P_{apr}(n) Papr(n)——时刻n n n的先验(预测)估计状态向量预测误差协方差矩阵。
2.1 预测(Prediction)步骤
当在 n − 1 n-1 n−1时刻得到测量数据时,先验状态( a priori state)和预测误差协方差估计(error covariance estimates)可以通过下式获得:
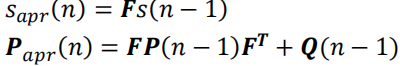
上述公式体现了卡尔曼滤波器的预测(Prediction)过程。其中的 Q ( n ) Q(n) Q(n)是过程噪声协方差矩阵。参加2.3节获取更多细节。
另外,我们使用第1节中的公式来计算预测状态对应的观测值向量 H ( sapr ( n ) ) H(s_{apr}(n)) H(sapr(n))。
2.2 更新步骤
当得到时刻 n n n时的测量值时,系统状态向量和预测误差协方差估计将通过下面的测量值更新过程进行更新:
a)利用观测向量 u ( n ) u(n) u(n)和状态估计向量 H ( sapr ( n ) ) H(s_{apr}(n)) H(sapr(n))计算观测误差(Compute innovation (or measurement residual))
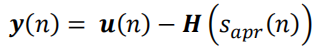
b)利用预测误差协方差 Papr ( n ) P_{apr}(n) Papr(n)和观测方差 R ( n ) R(n) R(n)计算更新误差协方差(Compute innovation(measurement residual) covariance)矩阵(用雅各比行列式代替观测矩阵 H H H)
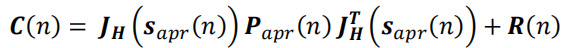
c)利用预测误差协方差 Papr ( n ) P_{apr}(n) Papr(n)和更新误差协方差 C ( n ) C(n) C(n)计算卡尔曼增益(Compute Kalman gain)
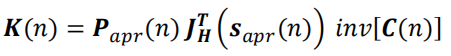
(d)根据测量误差 y ( n ) y(n) y(n)和卡尔曼增益 K ( n ) K(n) K(n)计算后验状态向量(Compute a-posteriori state vector)
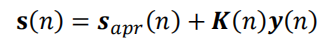
(e)更新后验预测误差协方差(Compute a-posteriori error covariance)矩阵
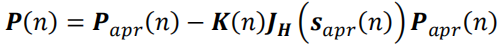
2.3 过程噪声矩阵 Q Q Q的设计
这部分借鉴了https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python中的相关内容。
Q ( n ) Q(n) Q(n)的选择对于卡尔曼滤波器的表现是非常重要的。如果Q设置的太小,那么滤波器将会对它的预测模型过于自信, 从而使其偏离真实情况。如果Q设置的过大,那么滤波器将会受到来自测量值噪声的较大影响,从而同样导致滤波器效果欠佳。
运动学系统(一个可以用牛顿运动方程建模的系统)是连续的,即它们的输入和输出可以在任何时间点上变化。然而,这里使用的卡尔曼滤波器是离散的。我们定期对这个系统进行采样。因此,我们必须找到上述方程中噪声项的离散表示。这取决于我们对噪音行为的假设。我们将考虑以下两种不同的噪声模型。
2.3.1 连续白噪声模型
假设我们需要建立位置,速度和加速度的模型。然后我们可以假设对于每个离散时间步长加速度是恒定的。当然,系统中有过程噪声,所以加速度实际上不是恒定的。随着时间的推移,被跟踪的物体会由于外部未建模的力而改变加速度。在这一节中,我们假设加速度随连续时间的零平均白噪声而变化。
由于噪声是不断变化的,我们需要利用积分运算来得到我们选择的离散区间内的离散噪声。这里我们将不再给出证明,噪声的离散化方程是
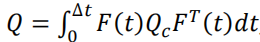
其中, Q c Q_c Qc是连续噪声。上式的基本思想应该是比较清晰的,即 F ( t ) Q c F T ( t ) F(t)Q_cF^T(t) F(t)QcFT(t)是连续噪声基于我们的过程模型 F ( t ) F(t) F(t)得到的时刻 t t t的映射。我们希望知道在一个离散区间 Δ t \Delta t Δt内,我们的系统会增加多少噪声,因此我们将表达式 F ( t ) Q c F T ( t ) F(t)Q_cF^T(t) F(t)QcFT(t)在区间 [ 0 , Δ t ] [0, \Delta t] [0,Δt]上积分。
对于二阶牛顿系统,状态转移矩阵为:

我们定义连续噪声为:
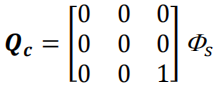
其中, Φ s \Phi_s Φs是白噪声的谱密度(spectral density),关于上述关系的证明已经超出了本文的范围。事实上,我们通常无法得知噪声的谱密度,因此该值变成了一个“工程”参数(“engineering” factor)——我们通常会调整该值直到得到理想的滤波器性能。我们可以看到与 Φ s \Phi_s Φs相乘的矩阵将噪声的功率谱密度有效地分配到了加速度部分。 这意味着我们假设:除了噪声造成的变化之外,我们的系统具有恒定的加速度,即噪声会改变加速度。
通过计算积分,我们得到:
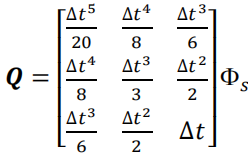
扩展到6个状态量的情况:
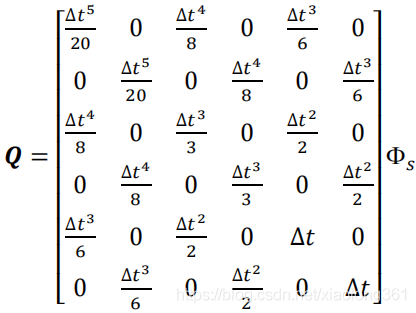
2.3.2 分段白噪声模型(Piecewise White Noise Model)
另一种噪声模型假设系统噪声带来的最高阶项(也就是,加速度)变化是分时间段恒定的,但是不同的时间区间内是不同的,且它们的值和所处的时间区间也是不相关的。换句话说,在每个时间区间之间,加速度存在一个非连续的阶跃(discontinuous jump)。这一点和2.3.1中提到的模型完全不同,上一节的模型中我们假设连续变化的噪声作用在最高阶项上。
我们将本节提出的模型定义为:
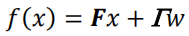
其中, Γ \Gamma Γ是系统的噪声增益, w w w是噪声带来的恒定的分段加速度(最高阶项,或为velocity,或为jerk,等)。
对于二阶系统:
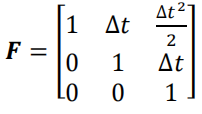
在一个时间区间内,加速度的变化为 w ( t ) w(t) w(t),速度的变化为 w ( t ) Δ t w(t)\Delta t w(t)Δt,且距离的变化量为 w ( t ) Δ t 2 / 2 w(t)\Delta t^2/2 w(t)Δt2/2。由此可知:
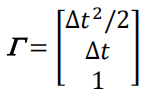
则过程噪声协方差矩阵为:
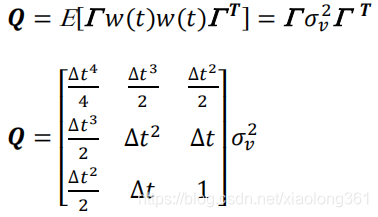
总之,很难说2.3.2中的模型是否比2.3.1中的模型更正确——他们两个都是对于现实中实际情况的近似。只有经验和试验(experience and experiments)可以让我们得到合适的模型。一般这两种模型都能够提供比较合理的结果,但通常其中一种会比另一种表现得更好。
第二种模型的优点是我们可以以 σ 2 \sigma^2 σ2的形式对噪声建模,这样我们就可以用运动或者我们预期的误差来描述噪声。第一种模型需要我们制定噪声的功率谱密度,这一点可能不是很直观,但是它更容易处理不同时间的采样值,因为噪声是根据时间区间积分得到的。然而,这些并不是固定的规则——使用任何模型(或你自己设计的模型)都要基于滤波器性能测试以及你对物理模型行为的了解。
一个比较好的经验是将σ \sigma σ设置为1 / 2 Δ α 1/2 \Delta \alpha 1/2Δα到Δ α \Delta \alpha Δα之间的值,其中Δ α \Delta \alpha Δα表示加速度在采样周期之间可能变化的最大值。实际工作中,我们一般会通过数据仿真,选取一个滤波器性能较好的σ \sigma σ值。
3 群组跟踪(Group Tracking)
3.1 顶层算法设计
随着毫米波雷达探测精度的提高,真实世界的毫米波雷达目标(汽车、行人、墙壁、着陆地面等)可以被检测为一系列的反射点,这些反射点将作为输入传递给跟踪处理层(tracking processing layer)。每个反射点都由距离、角度和径向速度等测量值组成。每个目标对应的多个反射点组成一个群组(group). 当然,任何时候都可能存在多个真实目标。因此,我们需要寻求一种能够处理多目标群组(multiple target groups)的跟踪器。
群组跟踪算法的实现思想如下图所示:
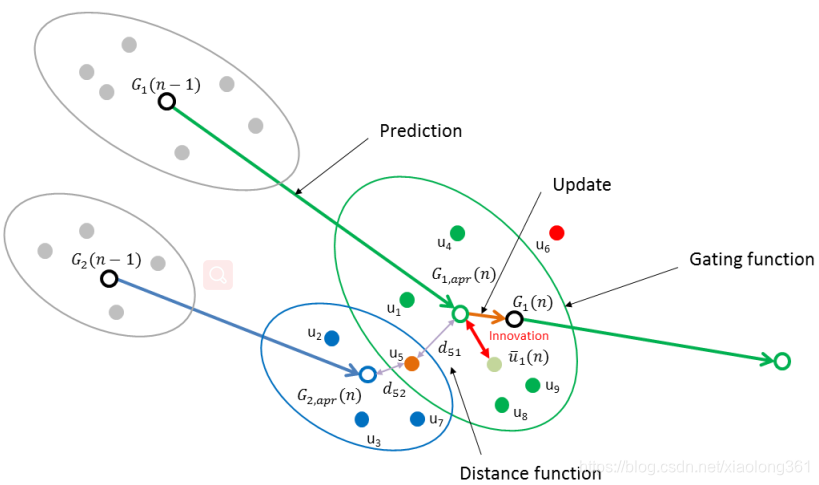
3.2 群组跟踪方框图
算法主要步骤的流程图如下所示:
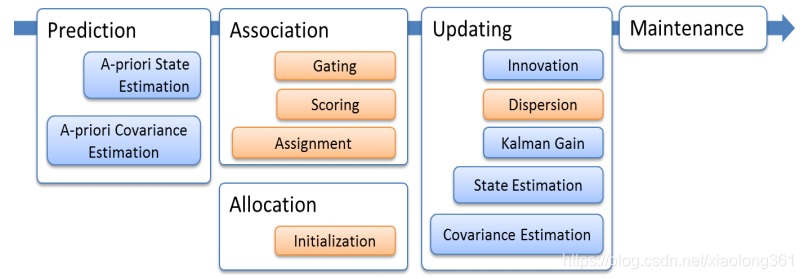
蓝色部分显示的函数为经典的**扩展卡尔曼滤波器(extended Kalman filter)**操作。棕色部分显示的函数为多目标聚类跟踪所需的附加函数。
3.3 预测过程(Prediction Step)
我们利用卡尔曼滤波器的预测过程基于时刻 n − 1 n-1 n−1的状态和过程噪声协方差矩阵来估计跟踪群组质心在时刻 n n n的状态。我们为每个跟踪目标得到一个先验状态( a priori state)和预测误差协方差估计(error covariance estimates)。同时在这一过程中我们也会计算预测状态对应的观测值向量 H ( sapr ( n ) ) H(s_{apr}(n)) H(sapr(n)),详细内容请参考本文2.1节。
3.4 关联过程(Association Step)
假设存在一个或多个轨迹和相关的预测状态向量。对于每一个给定的轨迹,我们形成了一个关于预测质心的门(Gate)。Gate应综合考虑目标机动性(Target maneuver)、群组的离散程度(Dispersion of the Group)以及测量噪声。
我们利用group residual covariance matrix——即更新误差协方差(Compute innovation(measurement residual) covariance)矩阵(参考2.2节(b))——建立了跟踪群三维测量质心的椭球体。椭球体将用来表示门限函数,以评判我们在时间n时观察到的测量值。Gate对应的门限函数(Gating Function)设计思路如下。
对于Gate内的观测值,我们计算归一化距离函数作为一个代价函数(cost function),以将观测值与每条轨迹关联起来。
分配过程(assignment process)将对代价函数进行最小化,每次将一个观测值分配到最邻近的轨迹。最终将为每个跟踪轨迹分配一系列观测值(即点云)。
3.4.1 门限函数(Gating Function)
门限函数表示在当前跟踪轨迹中存在的不确定性状态的前提下,我们愿意接受的测量误差(the amount of innovations).
为了对不确定性进行量化,我们定义群组残差协方差矩阵(group residual covariance matrix)如下:
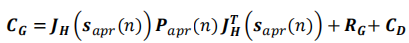
注意,该群组残差协方差矩阵 C G C_G CG是相对“观测值群组中的一个成员”和“群组质心”来说的。
比较上述群组残差协方差的计算公式和单一目标跟踪时的相应公式,我们可以发现:
术语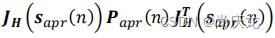
表示由于目标机动性(Target maneuver)带来的群组质心的不确定性,这和在单一目标跟踪时的术语类似。
术语 R G R_G RG表示测量误差协方差矩阵(measurement error covariance matrix),由于我们正在建立一个测量坐标系下的门限函数,因此我们不需要任何的转换。
最后,术语 C D C_D CD表示群组跟踪离散矩阵(group track dispersion matrix)的估计。
对于每个存在的跟踪轨迹 i i i,对于在时间 n n n获取的所有测量向量 j j j,我们定义距离函数 dij 2 d_{ij}^2 dij2,表示新的测量值添加到已有轨迹时的更新误差的大小(the amount of innovation)。
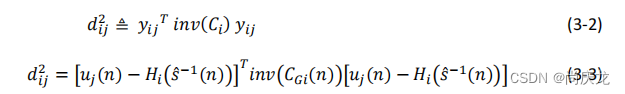
我们定义卡方测试(因为M个均值为零的高斯随机变量的平方和是自由度为M的卡方分布)来限制我们可以接收的更新误差的大小(the amount of innovation):

上述边界条件表示对于已存在的群组跟踪轨迹的质心观测值的先验估计,一个待关联观测值能被关联到该轨迹的条件是:当前观测值到群组质心的距离 dij 2 d_{ij}^2 dij2小于常数阈值 G G G。然而,对常数阈值 G G G的选择引出了稳定性问题。参考下面的图片。图中显示了两个在XY坐标系中具有相同门限中心并且G=16的椭球体。较大的椭球面表示 C G C_G CG矩阵具有较大离散度。因此,参数 G G G可以被认为是针对我们预期的 C G C_G CG矩阵带来的误差而设定的一个恒定的体积放大因子。现在,想象一下这个状态,如果群组轨迹与一个归一化距离相差很大但是依然可以接受的测量值相关联。这样带来的结果,就是使跟踪器变得更加离散,协方差矩阵增大,椭圆门限也会增大,从而导致更大距离的测量值被关联。反过来,随着更紧凑的测量,离散程度减小,也会导致门限椭圆体积越来越小。
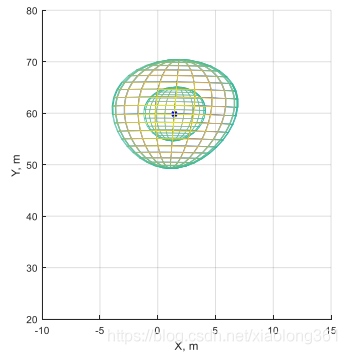
图6 椭球门限(G=16)
因此,提出的门控解决方案是基于定容概念。我们将寻找能够形成相同体积椭球体的门控函数。即给定恒定的体积 V V V,我们计算阈值 G G G。这样,具有较大离散程度的群组跟踪轨迹将会拥有更小的阈值 G G G,从而使更少的测量值被关联进来。最终这样的跟踪轨迹将会走向分裂,从而使其离散程度减小——这正是我们期望的行为。
3.4.2 打分函数(Scoring Function)
下图展示了观测值序列 u 1 , u 2 , u 3 , u 7 {u_1, u_2, u_3, u_7} u1,u2,u3,u7通过了绿色跟踪轨迹门限测试,观测值序列 u 3 , u 4 , u 5 , u 8 , u 9 {u_3, u_4, u_5, u_8, u_9} u3,u4,u5,u8,u9通过了蓝色跟踪轨迹门限测试的场景。
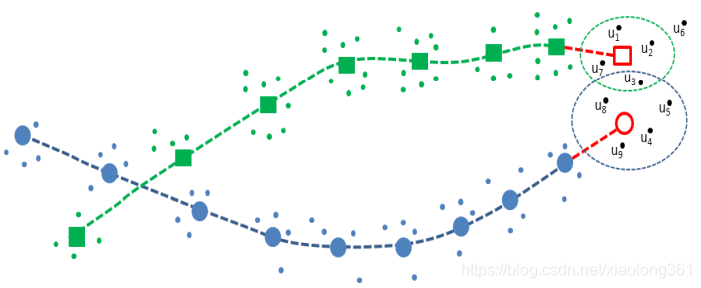
图7 打分函数图解
如参考文献【2】中所述,将观测值j分配给轨迹i的likelihood function(似然函数,假设残差符合高斯分布)如下:


3.5 分配过程(Allocation Step)
对于未关联到任何跟踪轨迹(处于任何一个已存在门限gate之外)的观测值,将为其分配并初始化一个新的群组跟踪器(group tracker)。这是一个迭代过程,类似于DBSCAN聚类算法。它要简单得多,因为它只对剩下的观测值来做。
我们首先选择一个最靠前的观测值,并设置一个等于它的质心(range/angle)。该观测值的径向速度用于进一步筛选其他候选观测值。每当有一个候选观测值,我们会检查这个点是否在速度范围内(即速度检查,在距离检查之后进行)。如果检查通过,则重新计算质心,并将点添加到该群组中。一旦完成该步骤,我们将为群组执行少数几个特定测试。我们可能需要检查群组中观测值的数量是否满足最小要求、组合信噪比SNR是否足够高,以及质心的动态性度量是否满足最小要求等。如果上述测试均通过,我们将创建(分配,allocate)一个新的跟踪对象,并使用群组中关联的观测值来初始化离散矩阵。关联观测值较少的群组将被忽略。
3.6 更新过程(Updating Step)
本过程和2.2节中的描述类似,下面只阐述其中的不同点。
跟踪轨迹基于在关联过程中被关联的观测值集合进行更新。对于每个跟踪轨迹,我们首先计算 u ˉ ( n ) \bar u(n) uˉ(n), 即所有关联观测值的均值。
然后, 我们计算跟踪轨迹状态估计值与跟它关联的所有观测值均值之间的残差:

然后,我们计算质心残差协方差矩阵:
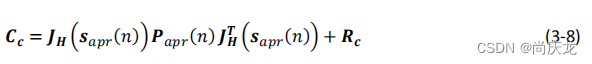
其中, R C R_C RC是质心观测值的误差协方差矩阵,由下式计算:

其中, R D R_D RD是雷达测量误差协方差矩阵,另外,

由上面的方程,测量噪声协方差矩阵是两个因子的和。前一部分表示质心的观测误差和雷达的观测误差呈正相关,并且它随着与质心相关联的反射点的测量值个数的增加而减少。第二个部分表示由于不一定所有的反射点都能被观察到,因此导致了一定的不确定性。我们定义权重因子用于对目标点漏检( N A < = N ^ N_A <=\hat N NA<=N^)的情况:

注意:该函数的限制:当 f = 0 f=0 f=0时,表示所有的关联观测值都被检测出来;当 f = 1 f=1 f=1时,我们只检测到了一个关联测量值。
我们将 N ^ \hat N N^作为一个配置参数,并且按照下面的方式递归的估计 C D C_D CD。
对于测量向量
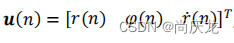 ,离散矩阵为:
,离散矩阵为:
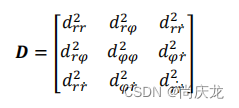
其中,
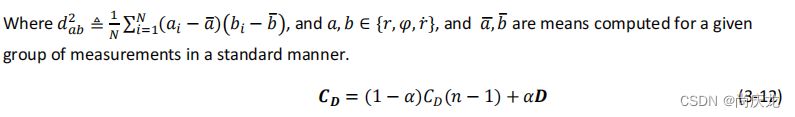
一旦 R C R_C RC被计算出来,剩下的步骤(计算卡尔曼增益、状态更新和协方差矩阵更新)将和2.2节中一致。
3.7 维持过程(Maintenance Step)
每个跟踪轨迹都拥有其生命周期。在维持过程中,我们可能会对不再使用的跟踪轨迹执行更改状态或删除操作。
4 执行细节
4.1 群组跟踪器(Group Tracker)
跟踪算法被封装到一个library中。应用task利用描述传感器、场景、雷达目标行为的配置参数创建一个算法示例。算法将在应用Task上下文中每个雷达处理帧被执行一次。也支持同时创建多个群组跟踪器实例。
下图解释了每帧调用过程中的算法执行步骤。算法的输入观测值数据位于极坐标系(range, angle, Doppler)中,跟踪目标处于笛卡尔坐标系(直角坐标系)中。因此我们使用EKF进行线性化处理。
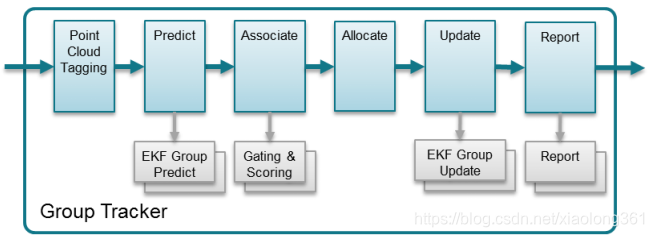
图8 群组跟踪器算法
雷达点云输入首先会基于场景边界( scene boundaries)配置进行标记。一些点云可能会被标记为“outside the boundaries”,从而在关联过程和分配过程中被忽略。
预测函数根据n-1时刻的系统状态和过程协方差矩阵来估计跟踪群组质心在n时刻的系统状态。我们为每一个可跟踪的目标计算得到一个先验状态和一个预测误差协方差矩阵。在这一步我们也会计算和状态估计值对应的观测估计值。
关联函数中会令每个跟踪单元判断每个观测点是否是在门限(Gating)范围内,如果是,就提供其相应的打分结果(scoring)。这些点会被赋予一个分值。没有被关联的点,则会经历分配过程。在分配过程中,点云首先会在观测坐标系下根据其接近程度被分为一个个集合。每个集合变成分配过程的一个候选。该集合必须符合多种阈值检查,才能变成一个新的跟踪轨迹。一旦该候选集合的检查通过,将针对该候选集合分配一个新的跟踪单元用于跟踪其轨迹。
在更新过程中,跟踪轨迹会根据一系列的关联观测值进行更新。我们会计算残差、卡尔曼增益,并更新后验状态向量和误差协方差矩阵。除此之外,和传统EKF不同的是,误差协方差的计算包含了观测噪声协方差矩阵中的群组离散信息。
报告函数查询每个跟踪单元并输出算法结果。
4.2 配置参数
配置参数用于配置跟踪算法。应该根据用户使用场景和目标特性对它们进行调整。参数被分为强制性配置和可选(高级)配置。
4.2.1 强制性的配置参数
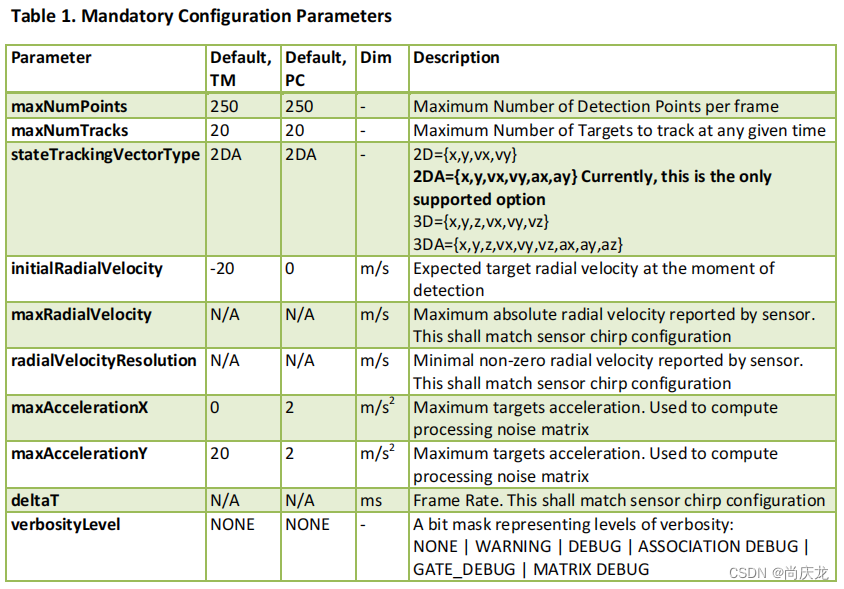
4.2.2 高级参数
高级参数被划分为多个部分。用户可以调整它们以获得更好的算法性能。
Scenery Parameters



Measurement Standard Deviation Parameters
该部分参数用于估计反射点观测值标准差。
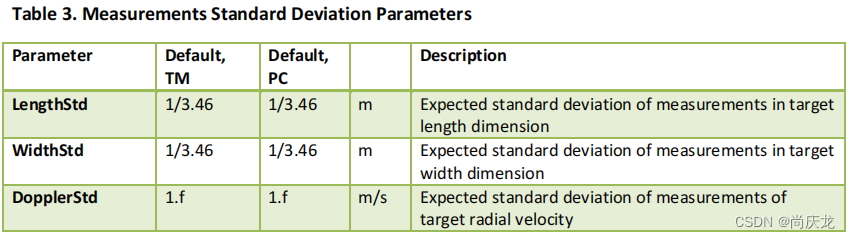

Allocation Parameters

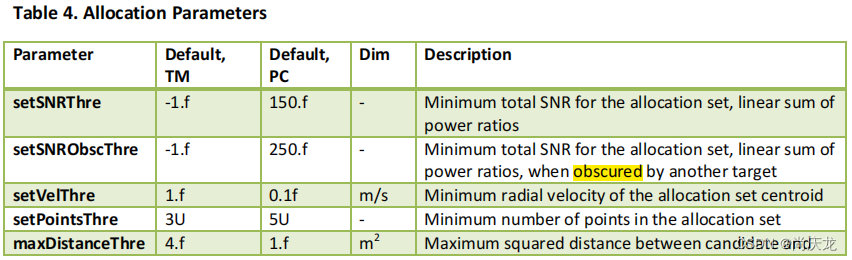

State Transition Parameters

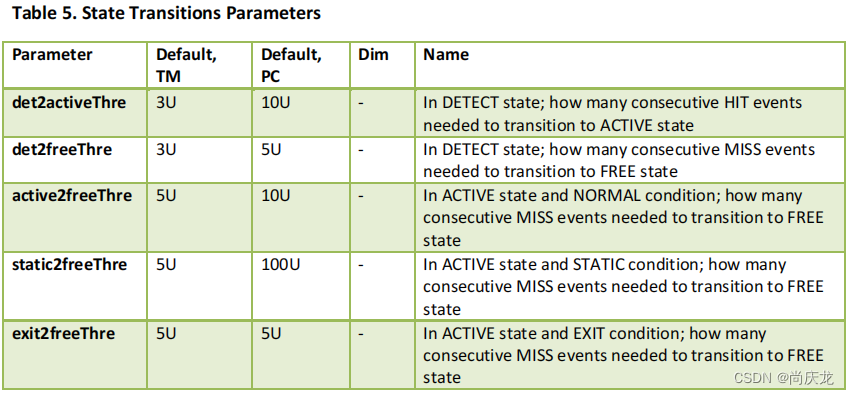
Gating Parameters
用于限制可以被关联到跟踪轨迹的观测点的边界限制条件,
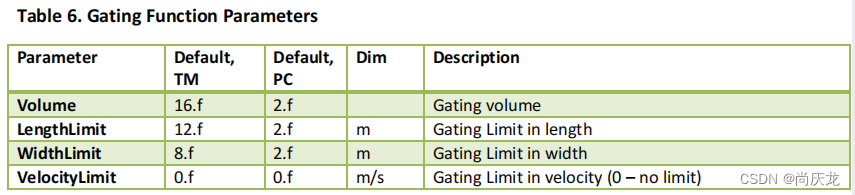

4.3 内存需求
用于250观测点+20跟踪轨迹的初试内存占用为80KB数据空间+20KB程序空间。
4.3.1 Data Memory
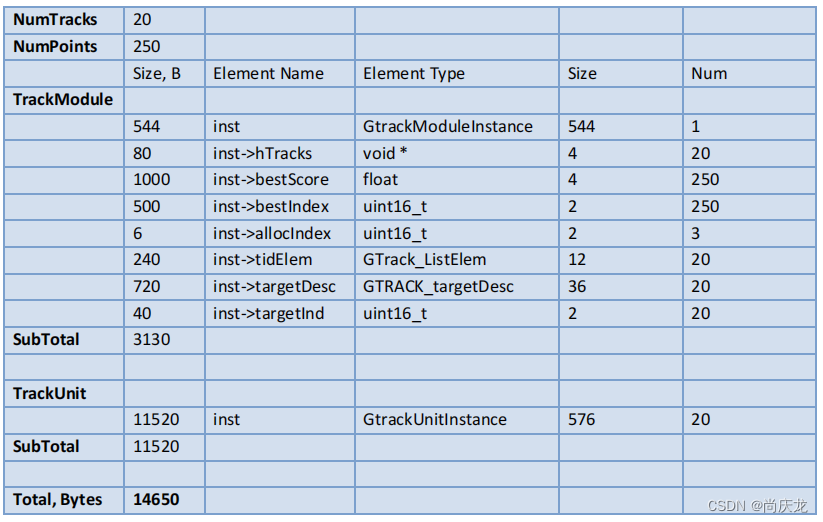
4.3.2 Program Memory
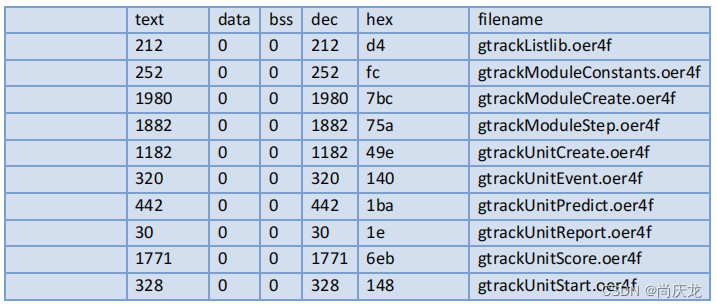
(接上表)
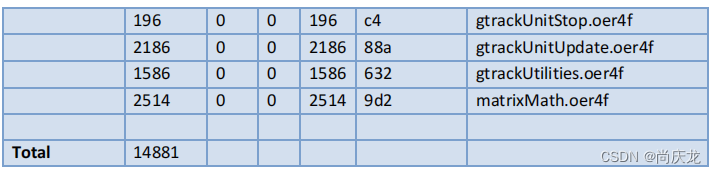
4,4 BenchMarks
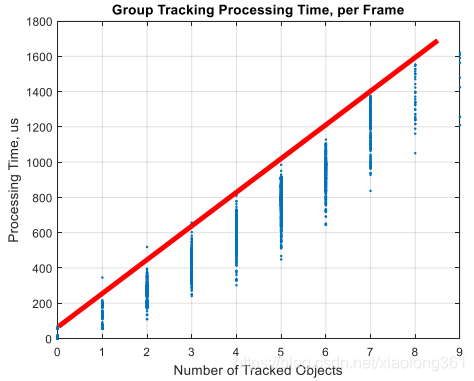
图:平均每跟踪一个轨迹处理耗时约200us
5 Performance
跟踪性能可以直观地用三类指标来表示——跟踪可靠性、跟踪精度、跟踪分辨率。

5.1 Tracking Reliability
跟踪可靠性的测试case类似于随机寿命试验。我们在交通检测使用场景下模拟跟踪性能试验。
5.1.1 Test Case描述
传感器的几何形状如下图所示。交通模拟采用随机泊松过程,车辆以随机速度进入四车道交叉路口。十字路口由交通灯控制,绿灯、黄灯和红灯的延时都是预先确定的。停止线在距离传感器20m处。车辆运动的建模规则如下:
- 每辆车保持恒定的速度,除非前面有障碍物。障碍物可以是前面的另一辆车,也可以是红色或黄色的交通灯。
- 前方有障碍物时,车辆会减速以配合障碍物的速度。减速量被限制到给定车辆类型允许的最大值。
- 车辆保持2米的安全距离。
- 障碍物一过,车辆就加速。每个车辆类型配置加速步长和最大加速量。
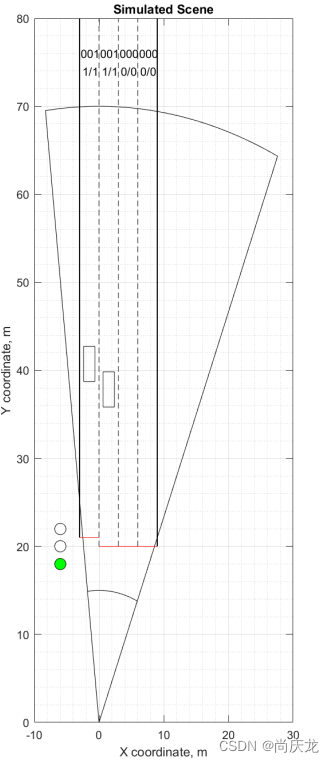
可靠性测试模拟了至少10分钟的交通。
传感器输出(点云)是随机生成的,并在移动车辆上获取测试数据后建模。该模型包括反射点数量的统计建模,点在距离/角度空间的分布,以及多普勒信息在点云中的分布。任意时刻的每个车辆都用点云(带有距离/角度和径向速度信息的反射点集)表示。
注:多个车辆产生的点云假设是累加的,因此我们没有对由于多个对象造成的点云退化建模。
对于点云合成,我们分别利用两种点云检测层配置分别采集了模拟测试的反射点,这两种配置如下:
- 配置A,具有“maximum possible”反射(单距离CFAR-CASO,多普勒维无窗口,0.2°DoA步长)
- 配置B,约1/3反射(双通程/多普勒CFAR-CASO, 0.2℃ DoA)
跟踪器输入点云,将反射点与被跟踪的对象关联起来,预测和建模对象的行为,并将估计的对象属性输出到上层。
上述每个配置都考虑以下两种测试case:
1)上层处理通过比较地面真实值( ground truth)和跟踪器输出来估计跟踪误差。对于地面真实值,我们考虑模拟车辆的矩形质心。对于每个跟踪轨迹,基于全局时间戳,我们对地面真值点结果和跟踪器输出结果进行同步处理。我们分别计算跟踪器存在的所有时间实例的均方误差。如果任何云点的均方误差没有超过期望的阈值,则表明对象跟踪正确,否则表明跟踪出现错误。
2)上层处理计数25米车道上的对象数量。这个计数也与地面真实数相比较。
5.2 结论
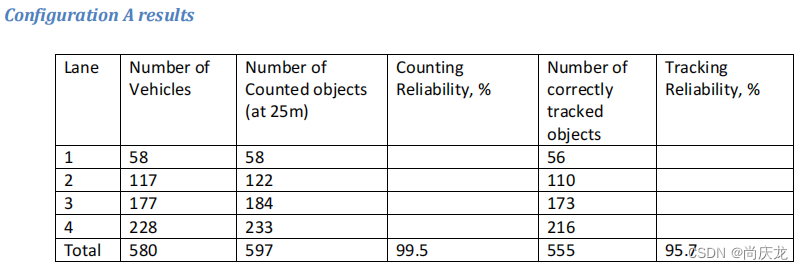
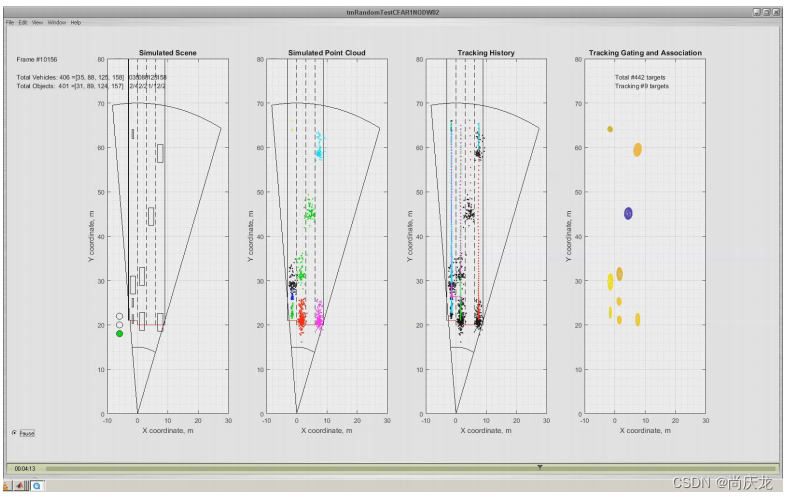
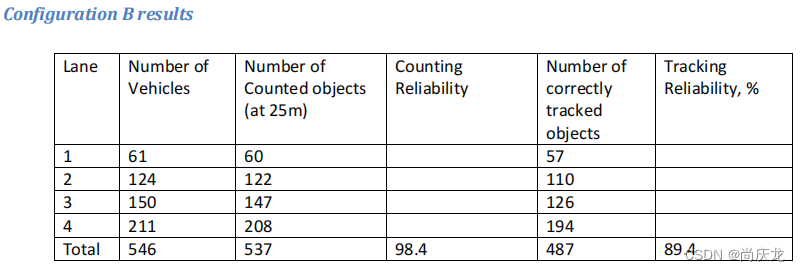
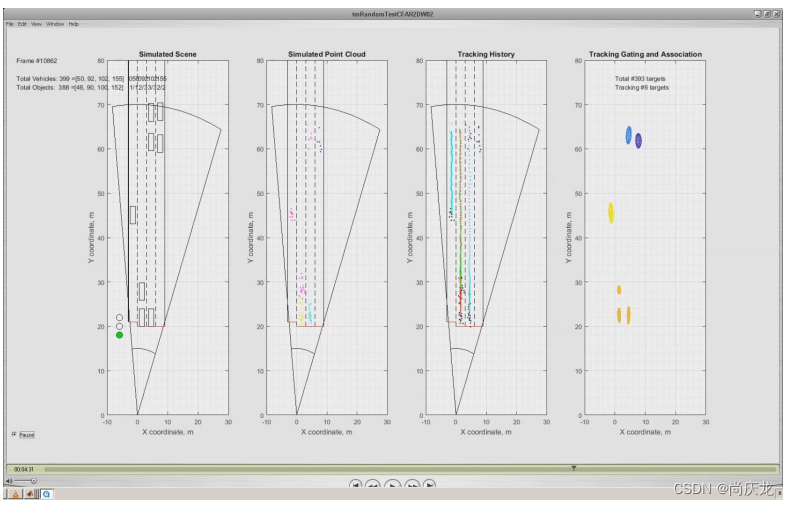
分析表明,绝大多数跟踪错误的原因主要包括以下两方面:
1)错误的分裂。例如,在一些场景下,跟踪器观察到一个群组中的离散程度过大,而将其分裂成了两个群组;
2)原始采集的误差,即轨迹开始时与地面真实值有较大偏差,收敛速度不够快。
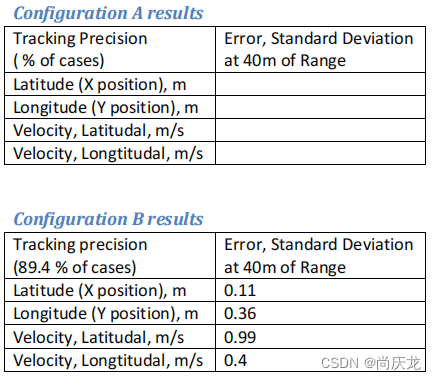
5.2 Tracking Precision
跟踪精度表示正确跟踪目标的特征估计的精确程度。这个分数不受追踪器识别和跟踪物体的能力的影响。对于正确跟踪的对象,我们计算:
- 位置跟踪精度。这是对匹配对象的期望位置误差(均值和偏差)的度量。展示了跟踪器估计物体位置的能力。
- 速度跟踪精度。这是对匹配对象的期望速度误差(均值和偏差)的度量。展示了跟踪器估计物体速度的能力。
- 尺寸跟踪进度。这是对匹配对象的期望尺寸误差(均值和偏差)的度量。显示了跟踪器估计对象大小的能力。
5.2.1 测试case描述
对于跟踪精度,我们使用与上面描述的相同的随机寿命测试用例。我们只选取“成功跟踪”的对象,并通过比较被跟踪对象与地面真实情况,得出这些情况下的误差统计。
5.3 Tracking Resolution
跟踪分辨率表示两个要单独跟踪的真实对象之间需要多少特征分离。特征分离可以用距离/角度/速度度量。我们为初始分离和动态分离设计了单独的测试用例。
5.3.1 初始分离
测试case描述
我们为距离、角度和径向速度分离设计了三个独立的测试用例。我们模拟具有以下特征的车辆进入场景:
a)距离差异(相同车道,两辆车,相同速度,在给定距离上一辆接一辆),
b)角度差异(相同range,不同车道,相同速度)
c)速度差异(相邻车道,最小角度差,不同速度)
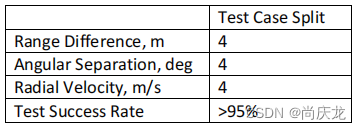
对于所有的测试,我们都寻求跟踪器能够区分两个目标,并在95%以上的情况下能成功地跟踪两个对象所需的最小差异。
测试结果

5.3.2 动态分离
测试case描述
设计了单独的测试case,测试刚开始时,两辆车是无法区分的。跟踪器应分配一个跟踪对象。但是,由于速度的差异,在几十帧之后,跟踪器应该能够触发分裂事件并跟踪两个目标。当跟踪器在>95%的情况下执行分离时,我们测量所需的分离量(在距离、角度和速度三个维度)。
测试结果
6 参考资料
【1】https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python
【2】Samuel S. Blackman. Multi-Target Tracking with Radar Applications, Artech House, 1986
【3】Muhammad Ikram, Nano radar DSP Algorithm Module, Tracking module description
7 Appendix
7.1 Evaluating Partial Derivatives
We need to calculate partial derivatives to compute Jacobian
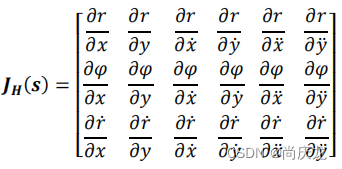


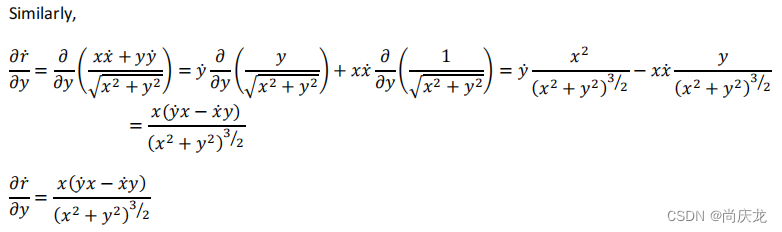


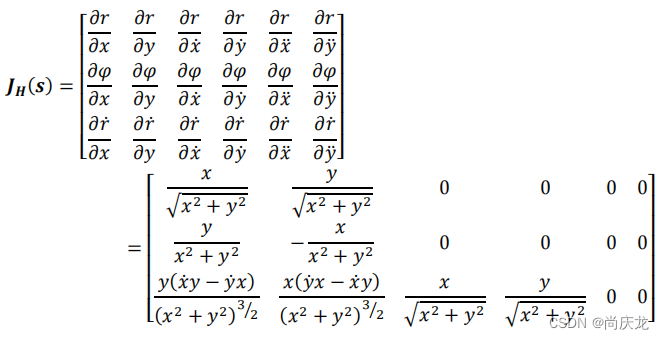
7.2 Orthogonal projection of an Ellipsoid E onto a given line