文章目录

• 堆(Heap)的基础知识
• • 堆排序伪代码
  • c++实现堆排序
• 精选算法题（Java实现）
• • 剑指Offer 最小的k个数
  • 最后一块石头的重量
  • 数据流的第K大元素
  • 查找和最小的K对数字
  • 丑数Ⅱ —— 就是只包含2、3和/或5的正整数
  • 超级丑数
  • 移除石子的最大得分
  • 前k个高频单词
  • 数据流中的中位数 —— 连续中值
  • 数组中的第K个最大元素

堆(Heap)的基础知识

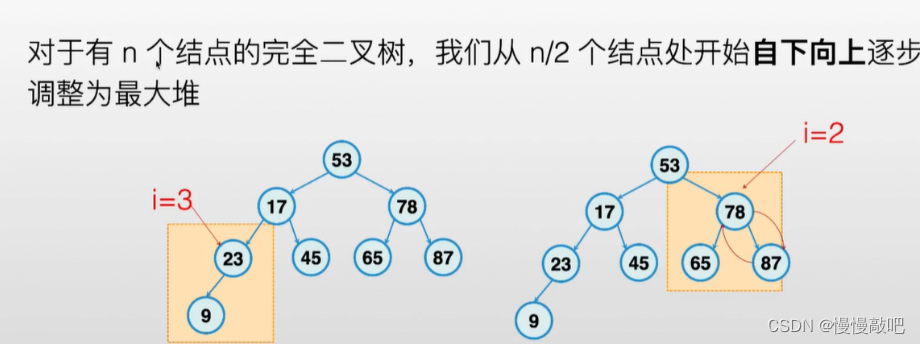
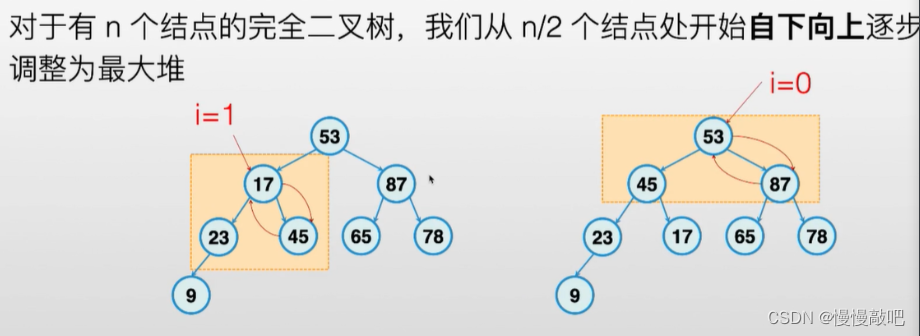
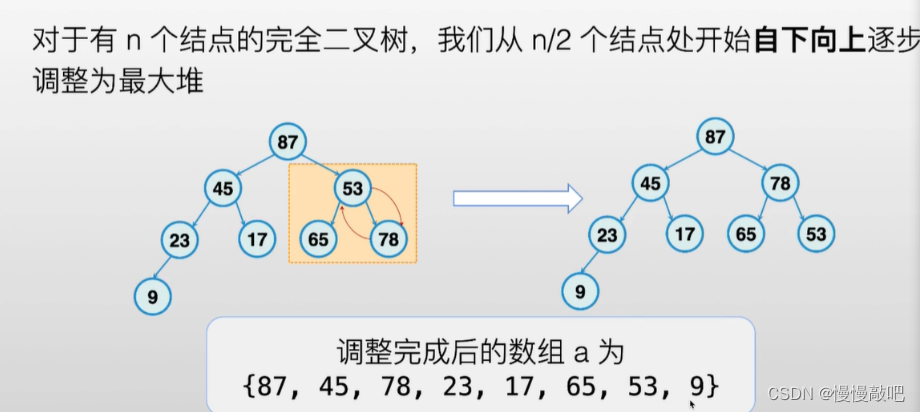
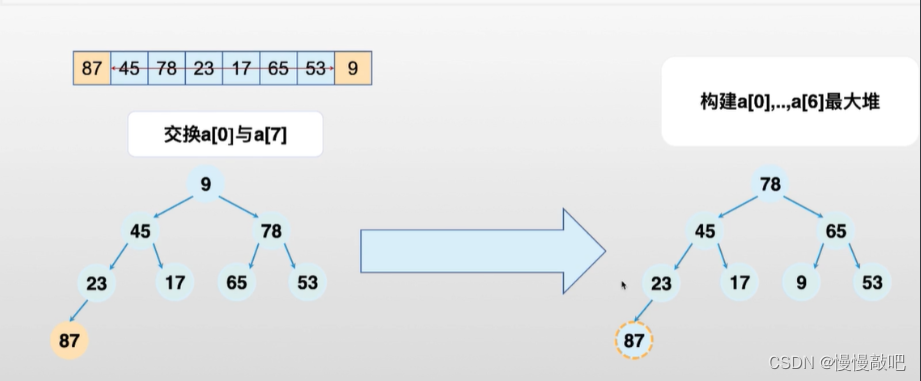
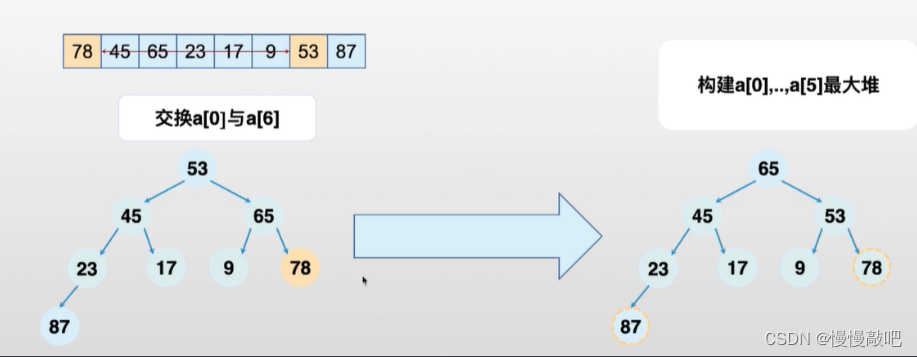
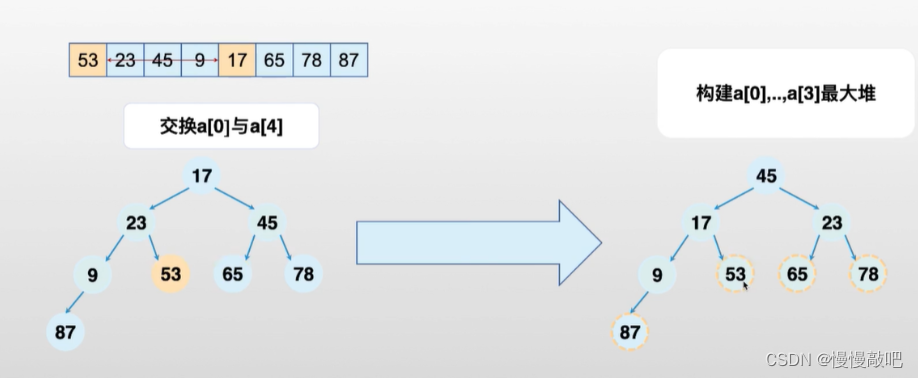
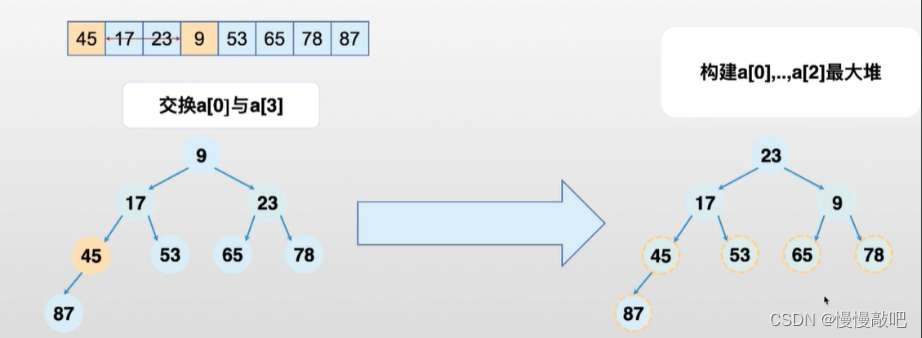
堆排序伪代码

c++实现堆排序

//大顶堆templateclass Heap{public:    Heap(){}    template    Heap(FuncT cmpFunc){ data = vector(); cmp = cmpFunc;    }    template    Heap(vector arr, FuncT cmpFunc){ data = arr; cmp = cmpFunc; heapify();    }    void push(T val){ data.push_back(val); siftUp(data.size() - 1);    }    T top() {return data[0];}    T top(){ T val = top(); data[0] = data[data.size() - 1]; data.pop_back(); siftDown(0); return val;    }    bool empty() { return data.empty();}    int size() { return data.size();}private:    //将data[idx]向上调整    void siftUp(int idx){ while(idx > 0 && cmp(data[idx], data[(idx - 1) / 2])){     //father = (idx - 1) / 2     swap(data[(idx - 1) / 2], data[idx]);     idx = (idx - 1) / 2; }    }    void siftDown(int idx){ while(idx * 2 + 1 < data.size()){     int lc = idx * 2 + 1;     int rc = idx * 2 + 2;     int tmpidx = idx;     if(lc < data.size() && cmp(data[lc], data[tmpidx])) tmpidx = lc;     if(rc = 0; i--){     siftDown(i); }    }private:    vector data;    function cmp;//传入的比较函数};int cmp(int a, int b){    return a > b;//此时为大顶堆}int main(){    vector a = {7,5,6,3,8,1,4,9,2};    Heap h{a, cmp}; while(!h.empty()){ printf("%d", h.pop());    }    printf("\n"); return 0;} 

void heap_sort(int[] a, int n){    int i; int t;    for(i = (n-2)/2; i >=0; i--){ siftdown(a,i,n);//调整为堆    }    for(i = n-1; i > 0; i-- ){ //进行堆排序 t = a[0]; a[0] = a[i]; a[i] = t; siftdown(a,0,i);    }}void siftdown(int[] a,int i,int n) {    int j;    int t = a[i];    while((j = 2*i + 1) < n){ //两子女中选大者 if(j < n - 1 && a[j] < a[j + 1])     j++; if(t < a[j]){     a[i] = a[j];     i = j; } else     break;    }    a[i] = t;}

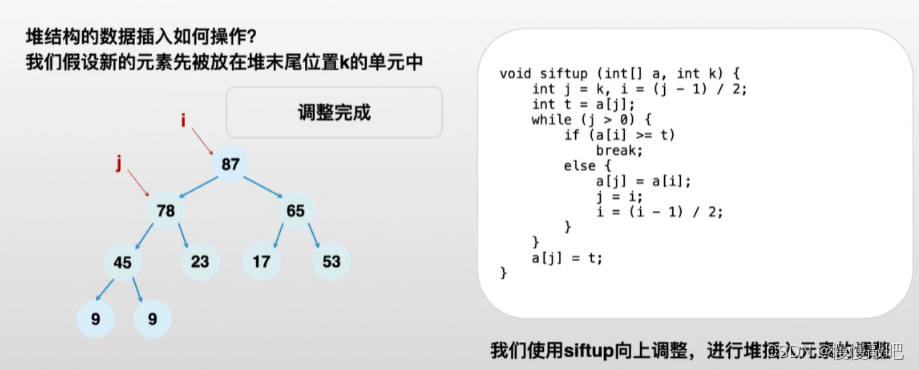
精选算法题（Java实现）

剑指Offer 最小的k个数

/** * 剑指Offer 最小的k个数 * @author: William * @time:2022-04-04 */public class Num40 {//快排public int[] getLeastNumbers2(int[] arr, int k) { quickSort(arr, 0, arr.length - 1); return Arrays.copyOf(arr, k);    }    private void quickSort(int[] arr, int L, int R) { // 子数组长度为 1 时终止递归 if (L >= R) return; // 哨兵划分操作（以 arr[l] 作为基准数） int i = L, j = R; while (i < j) {     while (i < j && arr[j] >= arr[L]) j--;     while (i < j && arr[i] <= arr[L]) i++;     swap(arr, i, j); } swap(arr, i, L); // 递归左（右）子数组执行哨兵划分 quickSort(arr, L, i - 1); quickSort(arr, i + 1, R);    }    private void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp;    }//利用小根堆public int[] getLeastNumbers(int[] arr, int k) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});for(int i : arr) {priorityQueue.offer(i);if(priorityQueue.size() > k) {priorityQueue.poll();}}return priorityQueue.stream().mapToInt(i -> i).toArray();    }//排序public int[] getLeastNumbers1(int[] arr, int k) {int[] vec = new int[k];Arrays.sort(arr);for(int i = 0; i < k; i++) {vec[i] = arr[i];}return vec;}}

最后一块石头的重量

/** * 最后一块石头的重量 * @author: William * @time:2022-04-04 */public class Num1046 {public int lastStoneWeight(int[] stones) {PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a);for(int stone : stones) {pq.offer(stone);}while(pq.size() > 1) {int x = pq.poll();int y = pq.poll();if(x > y) {pq.offer(x - y);}}return pq.isEmpty() ? 0 : pq.poll();    }}

数据流的第K大元素

/** * 数据流的第K大元素 * @author: William * @time:2022-04-05 */public class Num703{//用小根堆——因为要保留数据流中的前K大元素//使用小根堆能每次pop()最小的元素class KthLargest{PriorityQueue<Integer> pq;int k;public KthLargest(int k, int[] nums) {pq = new PriorityQueue();this.k = k;for(int num : nums) {//初始化一批王者add(num);//添加之后会自动排序}    } public int add(int val) {    pq.offer(val);    if(pq.size() > k) {    pq.poll();    }    return pq.peek();//返回第k大元素    }}}

查找和最小的K对数字

/** * 查找和最小的K对数字 * @author: William * @time:2022-04-05 */public class Num373 {public List<List> kSmallestPairs(int[] nums1, int[] nums2, int k) {//大根堆 —— 最后堆中就是想要的数据PriorityQueue pq = new PriorityQueue((int[] o1, int[] o2) -> o2[2] - o1[2]);//上面相当于//PriorityQueue pq = new PriorityQueue(new Comparator() {//@Override//public int compare(int[] o1, int[] o2) {//return o2[2] - o1[2];//}//});for(int i = 0; i < nums1.length; i++) {for(int j = 0; j < nums2.length; j++) {//人不够或者确实技术好一些if(pq.size() < k || nums1[i] + nums2[j]  k) pq.poll();//踢人的时候}else break;//如果这个不行那后面的更加不行，直接跳过(因为是升序排列)}}List<List> res = new ArrayList();while(!pq.isEmpty()) {int[] ints = pq.poll();res.add(new ArrayList() {{this.add(ints[0]);this.add(ints[1]);}});}return res;    }//多路归并boolean flag = true;    public List<List> kSmallestPairs2(int[] nums1, int[] nums2, int k) { int n = nums1.length, m = nums2.length; if (n > m && !(flag = false)) return kSmallestPairs(nums2, nums1, k); List<List> ans = new ArrayList(); PriorityQueue q = new PriorityQueue((a,b)->(nums1[a[0]]+nums2[a[1]])-(nums1[b[0]]+nums2[b[1]])); for (int i = 0; i < Math.min(n, k); i++) q.add(new int[]{i, 0}); while (ans.size() < k && !q.isEmpty()) {     int[] poll = q.poll();     int a = poll[0], b = poll[1];     ans.add(new ArrayList(){{  add(flag ? nums1[a] : nums2[b]);  add(flag ? nums2[b] : nums1[a]);     }});     if (b + 1 < m) q.add(new int[]{a, b + 1}); } return ans;    }}

丑数Ⅱ —— 就是只包含2、3和/或5的正整数

/** * 丑数Ⅱ —— 就是只包含2、3和/或5的正整数 * @author: William * @time:2022-04-05 */public class Num264 {//丑数都是丑数互相乘得到的public int nthUglyNumber(int n) {//创建小根堆，让丑数互相乘然后放进去PriorityQueue<Long> pq = new PriorityQueue<>();pq.offer(1L);//启动因子long ans = 0L;while(n-- > 0) {ans = pq.poll();if(ans % 5L == 0L) pq.offer(ans * 5L);else if(ans % 3L == 0L) {pq.offer(ans * 3L);pq.offer(ans * 5L);}else {//只包含2pq.offer(ans * 2L);pq.offer(ans * 3L);pq.offer(ans * 5L);}}return (int) ans;    }//动态规划//pi：有资格同i相乘的最小丑数的位置//这里资格指的是：如果一个丑数nums[pi]通过乘以i可以得到下一个丑数，//那么这个丑数nums[pi]就永远失去了同i相乘的资格（没有必要再乘了），//我们把pi++让nums[pi]指向下一个丑数即可。public int nthUglyNumber1(int n) {int[] dp = new int[n + 1];dp[1] = 1;int p2 = 1, p3 = 1, p5 = 1;for(int i = 2; i <= n; i++) {int num2 = dp[p2]*2, num3 = dp[p3]*3, num5=dp[p5]*5;dp[i] = Math.min(Math.min(num2, num3),num5);if(dp[i] == num2) p2++;if(dp[i] == num3) p3++;if(dp[i] == num5) p5++;}return dp[n];}}

超级丑数

/** * 超级丑数 * @author: William * @time:2022-04-06 */public class Num313 {//官方动态规划public int nthSuperUglyNumber(int n, int[] primes) {int[] dp = new int[n + 1];int m = primes.length;int[] p = new int[m];int[] nums = new int[m];Arrays.fill(nums, 1);for(int i = 1; i <= n; i++) {int minNum = Arrays.stream(nums).min().getAsInt();dp[i] = minNum;for(int j = 0; j < m; j++) {if(nums[j] == minNum) {p[j]++;nums[j] = dp[p[j]] * primes[j];}}}return dp[n];}public int nthSuperUglyNumber1(int n, int[] primes) {//质数应该去乘丑数列表中哪一个丑数int[] p = new int[primes.length];//丑数列表List<Integer> data = new ArrayList<>();data.add(1);int ans = 1;while(data.size() != n) {//丑数质数*丑数列表得到一系列丑数 //获取到这轮中丑数的最小值，加入到丑数列表中ans = primes[0] * data.get(p[0]);//每轮的第一个丑数for(int i = 1; i < primes.length; i++){ans = Math.min(ans, primes[i] * data.get(p[i]));}//根据获得的丑数，判断哪个质数在这轮中可以得到这个丑数//让他跳过这轮减少重复结果for(int i = 0; i < primes.length; i++) {if(primes[i] * data.get(p[i]) == ans) p[i]++;}data.add(ans);}return ans;    }}

移除石子的最大得分

/** * 移除石子的最大得分 * @author: William * @time:2022-04-06 */public class Num1753 {public int maximumScore(int a, int b, int c) {//存在两堆石子的个数之和小于等于另外一堆石子的个数时，//最大分数必然就是这两堆石子的个数之和。if(a + b <= c) return a + b;if(a + c <= b) return a + c;if(b + c <= a) return b + c;return (a + b + c) / 2;    }}

前k个高频单词

/** * 前k个高频单词 * @author: William * @time:2022-04-06 */public class Num692 {//哈希表排序public List<String> topKFrequent(String[] words, int k) {Map<String, Integer> count = new HashMap<>();for(String word : words) {count.put(word, count.getOrDefault(word, 0) + 1);}//用list存储字符key然后自定义Comparator比较器对value排序List<String> candidates = new ArrayList<>(count.keySet());candidates.sort((a, b) -> {// 字符串频率相等按照字典序比较使得大的在堆顶,Java 可以直接使用 compareTo 方法即可if(count.get(a).equals(count.get(b))) {return a.compareTo(b);}else {//字符串频率不等则按照频率排序return count.get(b) - count.get(a);}});//截取前K大个高频单词返回结果return candidates.subList(0, k);}//小根堆public List<String> topKFrequent1(String[] words, int k) {Map<String, Integer> map = new HashMap<>();//value —— 出现的次数for(String word : words) {map.put(word, map.getOrDefault(word, 0) + 1);}//构建小根堆 这里需要自己构建比较规则 默认实现小根堆PriorityQueue<String> pq = new PriorityQueue<>((o1, o2) -> {if(map.get(o1).equals(map.get(o2))) {return o2.compareTo(o1);}else {return map.get(o1) - map.get(o2);}});//依次向堆中加入元素for(String s : map.keySet()) {pq.offer(s);//当堆中元素个数大于k个的时候，需要弹出堆顶最小的元素if(pq.size() > k) pq.poll();}//依次弹出堆中的K个元素，放入结果集合中List<String> res = new ArrayList<String>(k);while(pq.size() > 0) {res.add(pq.poll());}//注意最后需要反转元素的顺序Collections.reverse(res);return res;//或者//PriorityQueue<Map.Entry> pq //= new PriorityQueue(new Comparator<Map.Entry>() {//@Override//public int compare(Map.Entry o1, Map.Entry o2) {//return o1.getValue() == o2.getValue() ? o2.getKey().compareTo(o1.getKey()) //: o1.getValue() - o2.getValue();//}//});//for(Map.Entry entry : map.entrySet()) {//pq.offer(entry);//if(pq.size() > k) pq.poll();//}//List res = new ArrayList();//while(!pq.isEmpty()) {//String key = pq.poll().getKey();//res.add(0, key);//}//return res;    }}

数据流中的中位数 —— 连续中值

/** * 数据流中的中位数 —— 连续中值 * @author: William * @time:2022-04-07 */public class Num295 {class MedianFinder {PriorityQueue<Integer> L, R;    public MedianFinder() {    //大根堆 —— 左半部分最大值    L = new PriorityQueue<Integer>((o1, o2) -> o2 - o1);    //小根堆 —— 右半部分最小值    R = new PriorityQueue<Integer>((o1, o2) -> o1 - o2);    } public void addNum(int num) {    if(L.isEmpty() || L.peek() > num) L.offer(num);    else R.offer(num);    if(R.size() > L.size()) {//右边多于左边    L.offer(R.poll());    }    if(L.size() == R.size() + 2) {//左边多于右边    R.offer(L.poll());    }    } public double findMedian() {    int n = L.size() + R.size();    if(n % 2 != 0) return L.peek();    return (L.peek() + R.peek()) / 2.0;    }}}

数组中的第K个最大元素

/** * 数组中的第K个最大元素 * @author: William * @time:2022-04-07 */public class Num215 {//第K个最大元素 —— k个里面最小的 —— 容量为k小根堆public int findKthLargest(int[] nums, int k) {PriorityQueue<Integer> pq = new PriorityQueue<>();for(int num : nums) {//可以加入的条件if(pq.size() < k || pq.peek() < num) {pq.offer(num);//堆中容量超过k就要吐出来if(pq.size() > k) pq.poll();}}return pq.poll();}//暴力解法 —— jdk默认快排public int findKthLargest1(int[] nums, int k) {int n = nums.length;Arrays.sort(nums);return nums[n - k];}}